|
Do not award half
marks. Do not deduct marks for trivial syntactic errors. Alternative
correct answers should be given credit, unless otherwise indicated
in the marking scheme.
(a)Explain what is meant by the following
terms:
(i)Array [2 marks ]
(ii)White box testing [2 marks ]
(iii)List [2 marks ]
(i) • A fixed
size data tructure;(1 mark)
• Elements can be accessed using indexing;(1 mark)
• Lookup time is constant;(1 mark)
• Update time is constant.(1 mark)
Note that a maximum of two marks are available [2 marks ]
(ii) • Testing all the possible logical paths through a system;(1
mark)
• Based on a knowledge of how the component work.(1 mark)
[2 marks ]
(iii) • Normally a variable size data structure;(1 mark)
• Indexing is performed from the front of the list;(1 mark)
• Lookup time is proportional to the length of the list;(1 mark)
• Update time is proportional to the length of the list.(1 mark)
Note that a maximum of two marks are available [2 marks ]
(b)(i)Explain how a binary search works.[3
marks ]
(ii)Explain how hashing works.[3 marks ]
(i)A binary earch works
by
• Comparing an item at the centre of the list with the search
term;(1 mark)
• Selecting the left or right sublist depending upon whether
the comparison
was greater or less than the search term;(1 mark)
• Continually repeating this process on the sublists until the
term is found.
(1 mark)
[3 marks ]
(ii)In hashing
• Every data item has an associated key value;(1 mark)
• Which is calculated using a specific hash function;(1 mark)
• Where the key value directly relates to the items storage location.(1
mark)
[3 marks ]
(c)Assume the following declaration of
a dynamic binary tree and the procedure FooBar

(i)Describe the effect of
FooBar on the root of a tree like the one above.[2 marks ]
(ii)Assuming an initially empty
tree,illustrate,with the aid of a diagram,the tree
resulting from the following code fragment:
Foobar(10);
Foobar(3);
Foobar(12);
Foobar(4);
[4 marks ]
(i)The
procedure FooBar will:
• Recursively try to add a data item to the leftmost leaf node
if it is greater
than the preceding node;(1 mark)
• And to the rightmost leaf node if it is greater than or equal
to the preceding
node.(1 mark)
[2 marks ]
(ii)The
tree will look as follow :
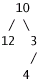
And
the following marking scheme should be used:
• Positioning 10 at the root of the tree;(1 mark)
• Positioning 12 a its left child;(1 mark)
• With 3 a the right child;(1 mark)
• And 4 as the left child of 3.(1 mark)
[4 marks ]
(d)(i)Define a type,called
MyType which can be used to store up to 50 real
numbers.[1 mark ]
(ii)Define a variable,MyVariable which consists of an array of 10
[1 mark ]
(i)TYPE MyType=
array[1..50] of REAL; [1 mark ]
(ii)MyVariable= array[1..10] of MyType; [1 mark ]
(e)Given the following declaration
of the type NUMTYPE
const max= 200;
TYPE NUMTYPE= array[1..max] of INTEGER;
(i)Using a while loop,write a procedure,called Initialise that takes
a its
argument a parameter of type NUMTYPE and initialises all the elements
of the
parameter to the value -1 [5mark ]
(ii)Write a recursive function Biggest which takes as it argument
a parameter of
type NUMTYPE and returns the largest element in the array.[5 marks
]
(i)A sample definition
of Initialise follows:
PROCEDURE
Initialise(VAR Num : NUMTYPE);
VAR index: INTEGER;
BEGIN
index:= 1;
WHILE(index<= max) DO BEGIN
num[index]:= -1;
index:= index+1;
END;
END;
And
the following marking scheme should be used:
• A correct procedure signature;(1 mark)
• Declaring a local index variable,and initiali ing it to 1;(1
mark)
• A correctly tructured WHILE loop;(1 mark)
• With the correct continuing condition;(1 mark)
• Initialising num[index] and incrementing index on each iteration.(1
mark)
[5 marks ]
(ii)A sample definition
of Biggest follows:
FUNCTION Biggest(num
: NUMTYPE, index : INTEGER) : INTEGER;
VAR temp : INTEGER;
BEGIN
IF index= 1 THEN Biggest:= num[1]
ELSE
BEGIN
temp:= Biggest(num, index-1);
IF num[index] > temp THEN
Biggest:= num[index]
ELSE
Biggest:= temp
END;
END;
And the following
marking scheme should be used:
• A correct function signature;(1 mark)
• Returning num[1] as the base case;(1 mark)
• Setting a local variable equal to the return value of the recursive
call;(1 mark)
• Testing the return value of this local variable against the
current element;
(1 mark)
• And returning the largest of the two.(1 mark)
[5 marks ]
|
