|
Do not award half
marks. Do not deduct marks for trivial syntactic errors. Alternative
correct answers should be given credit, unless otherwise indicated
in the marking scheme.
(a)Explain what is meant by a binary
search tree with respect to a binary
tree.[2 marks ]
A binary search tree
• Each subtree has two nodes;(1 mark)
• Where the subtree in one node will precede the items in another.(1
mark)
[2 marks ]
(b)Assume the following arithmetic expression:
A + B ˆ C /D
(i)Give the fully bracketed form of this expression.[2 marks ]
(ii)Draw a tree structure to represent the expression.[2 mark ]
(iii)Convert the expression into Pre-fix notation;[2 marks ]
(iv)Convert the expression into Post-fix notation.[2 marks ]
(i)A + ((B ^ C)/D)
One mark for knowing that ^ has a higher precedence than /, and one
mark for
knowing that / has a higher precedence than addition. [2 marks ]
(ii)The tree tructure should appear as follows:
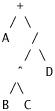
And one mark should be deducted for each incorrectly represented
structure.[2 mark ]
(iii)The Pre-fix expression should read:
+ A / ^ B CD
And one mark should be deducted for each error.[2 marks ]
(iv)The Post-fix expression should read:
A B C ^ D / + And one mark should be deducted for each error.[2 marks
]
(c)Assume the following definition of
a binary tree:
TYPE
BTreeNodePtr = ˆBTreeNode;
BTreeNode = RECORD
Left, Right : BTreeNodePtr;
Datum : INTEGER;
END;
Write a recursive procedure,called PrintCountTree
the signature of which is given below,which will perform a post order
traversal of the tree root printing out the value of Datum stored
at each node.
PROCEDURE PrintCountTree(root: BTreeNodePtr);
[5 marks ]
A
ample definition of PrintCountTree follows:
FUNCTION PrintCountTree(root: BTreeNodePtr) : INTEGER;
VAR left, right : INTEGER;
BEGIN
IF(!IsEmpty(tree)) THEN
BEGIN
left := PrintCountTree(rootˆ.Left);
right := PrintCountTree(rootˆ.Right);
Writeln(rootˆ.Data);
PrintCountTree:= 1 + left + right;
END
ELSE
PrintCountTree:= 0;
END
And the following marking cheme should be used:
• Testing that the node reached is non-empty before recursing;(1
mark)
• Printing out the value stored at each non-empty node;(1 mark)
• Recursing down the rightmost branch and then the leftmost branch;(1
mark)
• Returning 0 in the case of the empty tree (1 mark)
• Returning 1 + left + right in the non-empty tree case;(1 mark)
[5 marks ]
|