April 2000
MA214 : DISCRETE MATHEMATICS

QUESTION 3

Total Marks: 15 Marks

• Question 1
• Question 2
• Question 4
• Question 5
• Cover Page

SUGGESTED SOLUTIONS
Solutions and allocated marks are indicated in green.
Return to Question 3

(a) denotes the complete graph on n vertices,and denotes a cycle having n vertices.
[2 marks ]
[2 marks ]

(i)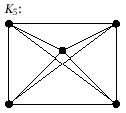
Two marks. Subtract one mark for every error up to a maximum of two. [2 marks ]
(ii)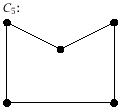
Two marks. Subtract one mark for every error up to a maximum of two. [2 marks ]

(b)How many edges do the following graphs have?
(i) [2 marks ]
(ii) 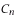[2 marks ]
(i)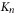 has n vertices.Each of these n vertices has n -1 edges leaving it.Each edge is attached to 2 vertices and so there are n(n -1 )/2edges.One mark for correct answer, one mark for justification. [2 marks ]
(ii)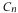 has n verices with 2 edges leaving each of these n vertices.Each edge is attached to 2 vertices and so there are n edges One mark for correct answer, one mark for justification..[2arks ]

(c)Consider the directed multigraph shown below.

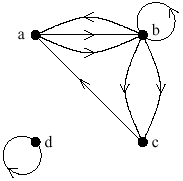
(i)List the vertices.
(ii)List the edges.
(iii)Find the in –degree and out –degree of each vertex.
[4 marks ]
(i)a, b, c, d One mark.
(ii)ab, ab, ba, bb, bc, bc, dd, ca One mark.
(iii)In degree:a =2,b =3,c =2,d =1.One mark.
Out degree:a =2,b =4,c =1,d =1.One mark.
[4 marks ]

(d)Consider the two graphs below.One graph is bipartite,the other is not bipartite. State,giving reasons,which graph is bipartite.For this bipartite graph find two sets of vertices A and B so that vertices within the same set are nonadjacent.[3 marks ]

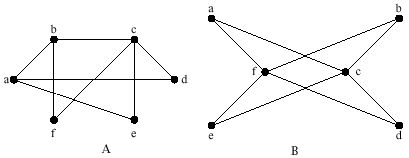
Graph B is bipartite.One mark. A ={c, f }and B ={a, b, d, e }.Two marks. Only award the mark for saying B is bipartite if the candidate has shown an understanding of what a bipartite graph is. [3 marks ]