|
(a)What is the minimum number of students needed to guarantee that
at least six students will receive the same grade,if there are five
possible grades A,B,C,D and F? Justify your answer.[4 marks ]
If
there are 5 grades available then by the generalised pigeon hole principle
the minimum number of students needed to guarantee that at least n
students receive the same grade is the smallest integer N such that
N =5 (n -1 ) +1.In this case, n =6,so N =26.One mark for the correct
answer, one mark for mentioning generalised pigeon hole principle,
two marks for the method. [4 marks ]
(b)A pair of fair dice are rolled.Let X be the sum of the numbers
that appear.Let S be the set of values that X can take.
(i)Write down the elements of S [2 marks ]
(ii)Write down the distribution of X .[5 marks ]
(iii)Calculate the expected value of X .[4 marks ]
(i)S ={2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10
, 11 , 12 }.Two marks. Deduct one mark for each error up to a maximum
of two. [2 marks ]
(ii)Distribution of X :

Five marks. Deduct one mark for each error up to a maximum of
five. [5 marks ]
(iii) 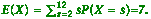
One mark for correct answer, three
marks for method. [4 marks ]
|
