Apr 1999 MA214: Discrete Mathematics (Question 1)

(a)	Let A be the null set.
	(i) What is the cardinality of A?	[1]
	(ii) What is the cardinality of the power set P(A)?	[1]
	(iii) What is the cardinality of the power set P(P(A))?	[1]
	(iv) List the elements of the power set P(P(P(A))).	[1]
	(i) Cardinality of A = 0 (ii) The power of set P(A) = {Æ} Cardinality of power set P(A) = 1 (iii) P(P(A)) = {Æ, {Æ}} Cardinality of power set P(P(A)) = 2 (iv) Elements of the power set P(P(P(A))) = {Æ, {Æ}, {{Æ}}, {Æ, {Æ}}}
(b)	Consider the following statement " basketball players x, x is tall Which of the following are equivalent ways of expressing this statement?	[2]
	(i) Every basketball player is tall.
	(ii) Some basketball players are tall.
	(iii) Some of all tall people are basketball players.
	(iv) Anyone who is tall is a basketball player.
	(v) All people who are basketball players are tall
	Every basketball player is tall. All people who are basketball players are tall.
(c)	(i) How many ways can the letters of the word DESIGN be arranged in a row?	[1]
	(ii) How many ways can the letters of the word DESIGN be arranged in a row if G and N must remain next to each other as either GN or NG?	[2]
	(i) No. of ways = 6! = 6 * 5 4 3 * 2 * 1 = 720 (ii) If GN is next to each other, No. of ways = 5! = 5 4 3 * 2 * 1 = 120 If NG is next to each other, No. of ways = 5! = 5 4 3 * 2 * 1 = 120 No. of ways if G and N must be next to each other = 120 + 120 = 240
(d)	Given the matrices , calculate the matrix (AB)^t .	[3]

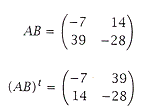(e)	Calculate the inverse of the function f(x) = 10 - 2x	[3]
	f(x) = 10 - 2x Let y = 10 - 2x y - 10 = -2x 2x = 10 - y x = (10 - y) / 2 f^-1(x) = (10 - x) / 2
(f)	Prove by induction that n³ - n is divisible by 6 for n ³ 1.	[5]
	Let n = 1, n³ - n = 1³ - 1 = 0 is divisible by 6. It is true for P(1). Assume that it is true for P(k) i.e. k³ - k is divisible by 6 for n ³ 1 We must prove that it is true for P(k + 1) i.e. (k + 1)³ - (k + 1) is divisible by 6 for n ³ 1 Proof: (k + 1)³ - (k + 1) = (k + 1)(k + 1)² - (k + 1) = (k + 1)(k² + 2k + 1) - (k + 1) = k³ + 2k² + k + k² + 2k + 1 - k - 1 = k³ + 3k² + 2k = k³ - k + k + 3k² + 2k = (k³ - k) + 3k² + 3k which is divisible by 6 for n ³ 1 \ We have proven that n³ - n is divisible by 6 for n ³ 1 by mathematics induction.
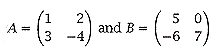