| (a) | A sprinter, a high jumper and a discus-thrower are to be chosen from a team of four athletes: Ann, Bob, Carol and Dan. No athlete may compete in more than one event. Ann cannot be the sprinter. Either Carol or Dan must be the discus thrower. How many different ways can the team be chosen? | [5] |
| 2C2
* 1C1 * 2C1 + 2C2 * 1C1
* 2C1 + 1C1 * 2C2 * 2C1
+ 1C1 * 2C2 * 2C1 = 1 * 1 * 2 + 1 * 1 * 2 + 1 * 1 * 2 + 1 * 1 * 2 = 2 + 2 + 2 + 2 = 8
|
||
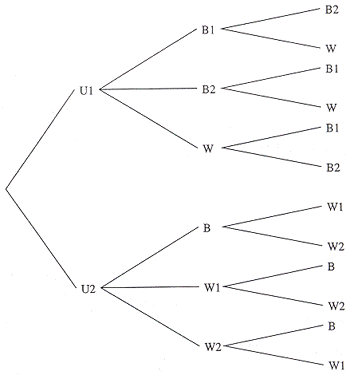
| (b) | An urn contains two black balls labelled B1 and
B2 and one white ball labelled W. A second urn contains one black ball labelled B and two
white balls labelled W1 and W2. The following experiment is performed: one of the two urns
is chosen at random and one ball and then a second are drawn without replacement from that
urn.
|
|
| (i) Construct a probability tree showing all possible outcomes of this experiment. | [4] | |
| (ii) What is the probability that two black balls are chosen? | [2] | |
| (iii) What is the probability that two balls of different colours are chosen? | [2] | |
| (i)
(ii) P(2 black balls) = (1/2 * 1/3
* 1/2) + (1/2 * 1/3 * 1/2) (iii) P(2 balls are different
colours) = 1/2[(1/3 * 1/2) + (1/3 * 1/2) +
|
||
| (c) | (i) Write down the formula for the number of ways of selecting k items of n different types if order does not matter and repetitions are allowed. | [2] |
| (ii) A camera shop stocks ten different types of batteries. How many ways can a total inventory of thirty batteries be distributed among the ten different types? | [2] | |
| (iii) One of the types of batteries is A76. How many ways can a total inventory of thirty batteries be distributed among the ten different types if the inventory must include at least four A76 batteries? | [3] | |
| (i) k - selection n + k - 1Ck = (n + k - 1)! / (n - k)! k! (ii) n = 10, k = 30 (iii) At least 4 types of batteries
are A76 so the additional 26 batteries are selected from 10 types. |