|
(a) State one similarity and one difference
between the nodes of a binary tree and an n-ary tree. [2 marks]
(a) • Both have only one parent node;
(1 mark)
• A binary tree has only two leaf nodes, an n-ary tree has n;
(1 mark)
[2 marks]
(b) Draw a tree structure to represent
the expression ( ((a + b) * c) ^d ) [3 marks]
(b) The tree should look like:
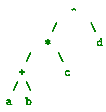
And the following marking scheme should be used:
• Correctly positioning ^sub expression as the root tree; (1
mark)
• * as the next sub expression, on its left; (1 mark)
• + as the next sub expression, on its left; (1 mark)
[3 marks]
(c) Given the following dynamic tree
structure, used to model arithmetic expressions:
TYPE BTreeNodeDatum= (Leaf, Plus, Minus);
TYPE BTreeNodePtr= ^BTreeNode;
BTreeNode= RECORD
Left, Right : BTreeNodePtr;
Datum : BTreeNodeDatum;
END;
Write a function, called Calculate, which will return the value of
an arithmetic expression given in the above binary tree format. [5
marks]
(c) A sample definition of Calculate follows:
Function Calculate(root : BTreeNodePtr) : Integer;
Begin
Case root.op of
Leaf: Calculate := rootˆ.Datum;
Plus: Calculate:= Calculate(rootˆ.Left)
+ Calculate(rootˆ.right);
Minus: Calculate:= Calculate(rootˆ.Left)
- Calculate(rootˆ.right);
End;
End;
And the following marking scheme should be used:
• A suitable function signature; (1 mark)
• A selection statement to identify the operator; (1 mark)
• Returning the data value when a leaf is reached; (1 mark)
• Applying an operator when one is found; (1 mark)
• To the correct subtrees; (1 mark)
(d) Given the following (alternative)
definition of a static binary tree:
TYPE BTreeNodeDatum = (Leaf, Plus, Minus);
TYPE BTreeNode = RECORD
LeftNodeIndex, RightNodeIndex : INTEGER;
Datum : INTEGER;
END;
BTree = ARRAY[1 .. MaxNodes] OF BTreeNode;
Write a function Position, the signature of which is given below,
which will traverse a tree of the type given above for a given entry
d, and will return the index in the array corresponding to the the
position of d. The LeftNodeIndex and teh RightNodeIndexin each BTreeNode
give the indices in the array of the left adn right subtrees respectively.
You can assume that a value of 0 for a left or right index indicates
there is no subtree on that node.
FUNCTION Position(rootTree: BTree;
d: INTEGER; currentNode: INTEGER): INTEGER; [5 marks]
(d) A sample definition of Position follows:
Function Position(root: BTree, d: Integer, currentNode: Integer) :
Integer;
Begin
if root[currentNode].Datum= d then
Position:= currentNode;
else begin
if root[currentNode].LeftNodeIndex != 0 then
Position := Position(root, root[currentNode].LeftNodeIndex,
d);
if root[currentNode].RightNodeIndex != 0 then
Position := Position(root, root[currentNode].LeftNodeIndex,
d);
Position:= 0;
end;
End;
And the following marking scheme should be used:
• Returning the array position if the element is found; (1 mark)
• Recursing with the leftmost branch if not; (1 mark)
• And then the rightmost; (1 mark)
• Correct arguments to the recursive calls; (1 mark)
• Returning 0 if the tree has been traversed without the element
being found; (1 mark)
[5 marks]
|