August 2000
MA214 : DISCRETE MATHEMATICS

QUESTION 1 (Compulsory)

Total Marks: 30 Marks

• Question 2
• Question 3
• Question 4
• Question 5
• Cover Page

Click to access
SUGGESTED SOLUTIONS
for Question 1

(a) A bag contains 4 red marbles, 6 blue marbles and 5 green marbles.
How many ways are there to choose 2 red, 4 blue and 3 green marbles from the
marbles in this bag? [3]

(b) Let R be the relation on the set Z+ of positive integers defined by aRb if and
only if a = b.
Prove or give a counter-example to determine whether R has the following
properties:
(i) reflexivity; [2]
(ii) symmetry; [2]
(iii) transitivity. [2]

(c) The matrices A and B are given by

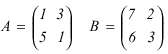
(i) Calculate AB [2]
(ii) Calculate BA [2]
(iii) Does (A + B)² = A² + 2AB + B² ? Justify your answer. [2]

(d) A function, f(n), defined for positive integers n, satisfies the following conditions:
f(1) = 2
f(n + 1) = 2f(n) for n = 1,2,3,...
Use mathematical induction to prove that f(n) = 2ⁿ for n = 1,2,3,.... [6]

(e) A man throws a die repeatedly until a six appears on the top face. Calculate the probability that:
(i) the first six appears on the second throw; [2]
(ii) the first six appears on the fourth throw given that a six does not appear
on the first two throws. [4]

(f) The sets A and B are defined by A = {1,2,3,4} and B = { x/x=y2,y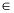 A} . Write down the members of the following sets:
(i) B [1]
(ii) A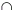B [1]
(iii) B- A[1]