Aug 1997 AP207: Advanced Programming Techniques (Question 1) Suggested Solutions

1.	(a) Briefly explain the following terms:
		(i) recursive procedure3		[2]
			a recursive procedure will contain a call to itself within the body of the procedure.
			some form of selection will be used to determine when to recursively call the procedure.
			any example of a recursive procedure.
			1 mark for each of the points above, to a maximum of 2 marks.
		[2 marks]
		(ii) queue		[2]
			an example of an abstract data type.
			supports FIFO (First-in, First-out) processing.
			contains at least two operations, enqueue and dequeue, to insert and remove elements from the queue.
			1 mark for each of the points above, to a maximum of 2 marks.
		[2 marks]
		(iii) abstraction		[2]
		abstraction: the physical properties of an item (how it works)		[1]
		are separated from its logical properties (how it is used).		[1]
		[2 marks]
		(iv) black box testing		[2]
			testing a module/program without any knowledge of the logic of the program.	[1]
			tests to see if the right outputs are achieved using the inputs provided.	[1]
		[2 marks]
		(v) binary search		[2]
		a search procedure that splits the search space into two parts,		[1]
		and searches one or both of the resultant parts, depending upon the application, using the same, recursive, procedure.		[1]
		[2 marks]

	(b) Write a Pascal type definition that models the following data-structure:			[3]

	Declaration of the tree type as follows.

	The student should not be penalised for using different names for Data, Left, Right, Up, Down, Pointer, NodeType, or Pointer.
	[3 marks]

	(c) Pascal does not contain a power operator (i.e., x^y). Write a function power that takes two parameters x and y and calculate x^y. You need not use recursion in the definition of power.			[3]
	A recursive definition of power is shown below:

	and the following marking scheme should be used:
		one mark for identifying the base case correctly. i.e., return 1 when y is less than 1. No marks should be deducted if the students just identify the conditional for the base case as y=0.
		one mark for the term x in the expression that is part of the recursive case of the function definition.*
		one mark for identifying the correct recursive call power (x, y - 1)
		no marks should be deducted for trivial syntactic errors.
	Alternatively, the students may use iteration in a definition as follows:

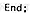	and the following marking scheme should be used:
		one mark for identifying that the variable that holds the result of the function should be initialised to 1.
		one mark for the definition of a for - do statement that contains y iterations.
		one mark for changing the value of the result variable power by multiplying by x.
	[3 marks]

	(d) Use the function power in the definition of a recursive function addPower that takes a single positive integer value n as a parameter, and returns an integer that is the sum of the following series:			[4]
		f(n) = 1¹ + 2² + 3³ + . . . + nⁿ
	A recursive definition of the addPower function is shown below:

	Four marks should be awarded for the definition as follows:
		one mark for a correct function definition. i.e., identifying that addPower takes an integer parameter n and returns an integer as a result. No marks should be deducted if the Procedure keyword is used in preference to Function, as long as a return type is given.
		one mark for identifying a correct base case for the recursion. i.e., one is returned from the function when n is less than or equal to one.
		one mark for identifying that the power function power (n, n) is required at each iteration of the recursion.
		one mark for the recursive case of calling addPower (n - 1).
		no marks should be deducted for trivial syntactic errors (i.e., missing semi-colons; using = instead of := in an assignment; missing Begin/End statements). No marks should be deducted if the recursive case contains a statement of the form: addPower := power (n, n) + addPower(n - 1);
	[4 marks]