| 2. |
(a) Using fixed point
arithmetic with 2's complement representation, calculate the result of the
following sum: |
[4] |
|
|
-16 - 64 = ? |
|
|
Convert the final result to decimal. |
|
|
| 16 |
= |
00010002 |
| -16 |
= |
111100002 |
|
|
|
one mark |
|
|
| 64 |
= |
010000002 |
| -64 |
= |
110000002 |
|
|
|
one mark |
|
|
|
|
|
one mark for a
correct addition |
|
|
|
|
|
one mark; no
mark if not converted |
|
|
[4
marks] |
|
|
|
|
|
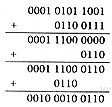
(b) Perform the BCD addition
of 15910 and 6710. Convert the final result to decimal. |
[4] |
|
|
 |
|
|
one mark for a
correct addition, one mark for the first correction - to adjust for the carry ---, and one
mark for the second correction --- to adjust for the representation |
|
|
|
= 22610 |
|
|
one mark for
the correct answer --- that is, the effect of the two adjustments and the translation into
decimal; no mark if not converted. |
|
|
[4
marks] |
|
|
|
|
|
(c) Using floating point
arithmetic with 2's complement representation, a 6-bit mantissa, and a 4-bit
exponent, calculate the result of the following sum: |
|
|
|
-231.124 - 1B.816
= ? |
|
|
|
231.124
|
|
|
|
|
= 0010 1101 01102 |
|
|
|
|
= 0.10 1101 0110 * 26 |
|
|
|
|
= 01011 0101 |
|
|
one mark for
correct conversion to binary; one mark for correct translation in 6-4 format |
|
|
|
-231.124 =
101010 0110 |
|
|
one mark for
negation in 2's complement |
|
|
|
1B.816 |
|
|
|
= 0001 1011.10002 |
|
|
|
|
= 0.11 011 10 * 25 |
|
|
|
|
= 011011 0101 |
|
|
one mark for
correct conversion to binary; one mark for correct translation in 6-4 format |
|
|
|
1B.816 |
|
|
|
|
= 100101 0101 |
|
|
one mark
for negation in 2's complement |
|
|
|
|
= 110010 0110 |
|
|
one mark for correct
rescaling of smaller exponent |
|
|
|
|
|
Convert the final result to decimal
representation and comment upon the accuracy of the answer. |
[12] |
|
|
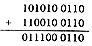 |
|
|
one mark
for a correct addition |
|
|
|
|
= 011100 * 26
= 1110002 = 5610 |
|
|
one mark
for correct translation of exponent; one mark for correct translation to binary; one mark
for translation to decimal representation |
|
|
The
answer is wrong because an overflow occurred. One mark for this explanation. |
|
|
[12
marks] |
|
