Aug 1999 AP207 : Advanced Programming Techniques (Question 1) Suggested Solutions

(a)	Briefly explain the following terms : (i) Sorting (ii) Searching (iii) White box testing (iv) Black box testing	[1] [1] [1] [1]
	(i) Sorting is the action of arranging elements of data into a defined order. (ii) Searching is looking through a collection of data for a particular item of data. (iii) White box testing is a module or program using a knowledge of its internal workings to see if the outputs are correct given the inputs. (iv) Black box testing is testing a module or program without a knowledge of its internal workings to see if the outputs are correct given the inputs.
(b)	(i) Explain, informally, how a selection sort works, and state how many passes of an unsorted list of length N it will take to ensure the list is sorted. (ii) Explain, informally how a binary search works, and state the maximum number of passes it will take over a list of length N to find an item.	[3] [3]
	(i) A selection sort works by: Moves the first unsorted item in a list to the beginning of the list; by exchanging it with the first item in the list. N-1 passes will be required. (ii) A binary search works by: Comparing the value in the middle of the list with the key, and sub dividing this search to the lower half if it is grater, or the upper half if it is less, Until the element is found, or the list cannot be further sub-divided. At most, 1 + log2N will be required.
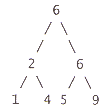
(c)	Given the following definition of a binary tree, and the procedure FooBar TYPE TreeType: ^TreeNode; TreeNode = RECORD left : TreeType; data : Integer; right : TreeType; END; PROCEDURE (FooBar VAR root : TreeType; item : Integer) Begin IF root == Nil THEN BEGIN New(root); Root^.data :=item; Root^.left:=Nil; Root^.right:=Nil; END ELSE IF item < root^.data THEN FooBar(root^.left, item) ELSE FooBar(root^.right, item); END; (i) Describe the effect of the procedure FooBar on the root of a tree like the one above. (ii) Assuming an initially empty tree, illustrate, with the aid of a diagram, the tree resulting from the following code fragment : Foobar(6); Foobar(2); Foobar(6); Foobar(4); Foobar(9); Foobar(1); Foobar(5);	[2] [4]
	(i) The procedure FooBar will: Recursively try to add a data item to the leftmost leaf node if it is less than the preceding node; And to the rightmost leaf node if it is greater than or equal to the preceding node. (ii) The tree will look as follows:
(d)	Write a recursive function, Power, which takes two integer arguments, x and y, and returns x^y. You can assume that both parameters will be greater than zero.	[4]
	A sample definition of Power follows: FUNCTION Power(x, y: Integer) : Integer BEGIN IF y== 0 THEN Power:= x; ELSE Power:= x*Power(x, y-1); END;