Aug 1999 AP207 : Advanced Programming Techniques (Question 5) Suggested Solutions

This question is concerned with the implementation of a sorting procedure that uses the insertion sort algorithm. The definition of a linked list type, a prototype for the procedure Insert, and the procedure InsertionSort are given below. 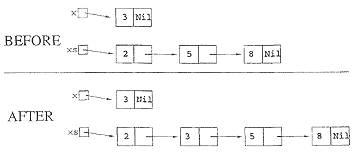Type List = ^Node; Node=RECORD Item : Integer; Next: List END; PROCEDURE Inset(x : List; VAR xs : List); PROCEDURE InsertionSort (VAR xs : List); VAR rest, singleton, result : List; BEGIN rest : =xs; result := Nil; WHILE (rest <> Nil) DO BEGIN singleton : = rest; rest : = rest^.Next; singleton^.Next : = Nil; Insert(singleton, result); END xs:= result END; The procedure insert (to be defined later) takes a singleton list x and a sorted xs as its arguments, and inserts the element stored in the singleton list into the sorted list such that the list xs remains sorted. For example, the figure below shows an example list before and after adding the singleton element 3 :
(a)	Informally describe the insertion sorting algorithm used in the Pascal procedure InsertSort above.	[3]
	identifying that a temporary list that will contain all sorted elements is built incrementally from an empty list. identifying that N insertions will occur(where N is the length of the list to be sorted). Alternatively, the students may say that every element in the list to be sorted is traversed, and inserted into the temporary list. that insert is used to place each element in the temporary sorted list.
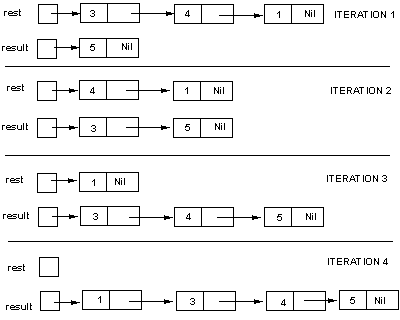
(b)	Given the list [5,3,4,1], draw four diagrams that show the states of the lists rest and result immediately after each execution of insert.	[8]

(c)	How many list elements would have to be traversed by all the invocations of the insert procedure given: (i) an already sorted list of size N passed to InsertionSort? i.e., what is the worst case cost, or upper-bound complexity of insertion sort? (ii) a list in decreasing order of values of size N passed to InsertionSort? i.e, what is the best case cost, or lower-bound complexity of insertion sort?	[1] [1]
	(i) N², or, o(N²) (ii) N, or O(N)
(d)	Define the procedure Insert.	[7]
	A definition of Insert is shown below: PROCEDURE Insert(x: List; VAR xs: List); VAR temp, drag: List; BEGIN IF (xs = Nil) THEN xs := x; ELSE IF (xs^.Item > x^.Item) THEN BEGIN x^.Next := xs; xs := x END ELSE BEGIN temp := xs; drag := Nil; WHILE ( (temp <> Nil) AND (x^.Item > temp^.Item) DO BEGIN drag := temp; temp := temp^.Next END; x^.Next := temp; drag^.Next := x; END END;