December 1998
SW204: SOFTWARE AND FILES DESIGN

QUESTION 2

Total Marks: 20 Marks

 Click here to access other questions

SUGGESTED SOLUTIONS
Solutions and allocated marks are indicated in green.
Return to Question 2
2. (a) With the aid of an example, describe how deadlock can occur when two processes are competing for resources.
 [4]

Marks should be awarded on the following basis:

  • Four marks should be awarded if the candidate provides an example which illustrates deadlock, and describes how deadlock occurs in the example.
  • Three marks should be awarded if the candidate provides an example which illustrates deadlock and provides a definition of deadlock (but does not illustrate how it occurs in the example).
  • Two marks should be awarded if the candidate provides an example which illustrates deadlock, but without an explanation of how it occurs.
  • One mark should be awarded if the candidate demonstrates a slight grasp of the subject matter (e.g. there is an attempt at a diagram involving resources and processes, but no deadlock).

No marks should be awarded otherwise.

 

 [4]

(b) Name two strategies which may be employed in handling deadlock.

 [2]

One mark should be awarded for each valid point (up to a maximum of two marks). Examples include the following:

  • Deadlock detection and recovery.
  • Deadlock avoidance.
  • Deadlock prevention.

Other sensible answers should also receive credit.

 

 [2]
(c) Distinguish between the terms job scheduler and CPU scheduler.
 [2]
A job scheduler is responsible for admitting jobs into the system (1 mark), whereas a CPU scheduler allocates CPU time to jobs in the ready queue (1 mark).

Other sensible answers should also receive credit.

 

 [2]

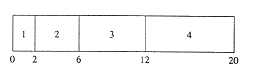
(d) Suppose, in a multiprogramming environment, a processor is assigned the following jobs for execution.

Job

Arrival Time

CPU Time

Priority

1

0

2

4

2

1

4

2

3

2

6

3

4

3

8

1

Priority is highest for 1 and lowest for 4.

Draw a Gantt Chart to illustrate the execution of these jobs using the following scheduling algorithms.

 [6]
(i) First come first served.
 [1]

Two marks should be awarded for a correct Gantt chart; one mark should be awarded if there is a minor slip in labelling; no marks should be awarded otherwise.

pic1s.gif (2686 bytes)

 

 [2]
(ii) Round robin, with a time quantum of 2.
 [2]

Two marks should be awarded for a correct Gantt chart; one mark should be awarded if there is a minor slip in labelling; no marks should be awarded otherwise.

pic2s.gif (8413 bytes)

 [2]
(iii) Priority scheduling.

Two marks should be awarded for a correct Gantt chart; one mark should be awarded if there is a minor slip in labelling; no marks should be awarded otherwise.

pic3s.gif (5492 bytes)

 

 [2]
(e) For each of the algorithms mentioned in part (b), compute the average waiting time.
 [6]
(i) The waiting time for 1 is 0, the waiting time for 2 is 1, the waiting time for 3 is 4, and the waiting time for 4 is 9 (1 mark). Therefore, the average waiting time is 14/4 = 3.5 (1 mark).

 

 [2]
(ii) The waiting time for 1 is 0, the waiting time for 2 is 1 + 4 = 5, the waiting time for 3 is 2 + 4 + 2 = 8, and the waiting time for 4 is 3 + 4 + 2 = 9 (1 mark). Therefore, the average waiting time is 22/4 = 5.5 (1 mark).

 

 [2]
(iii) The waiting time for 1 is 18, the waiting time for 2 is 8, the waiting time for 3 is 11, and the waiting time for 4 is 0 (1 mark). Therefore, the average waiting time is 37/4 = 9.25 (1 mark). [2]