December 1999
AP207 : ADVANCED PROGRAMMING TECHNIQUES

QUESTION 2

Total Marks: 15 Marks

• Question 1
• Question 3
• Question 4
• Question 5
• Cover Page

SUGGESTED SOLUTIONS
Solutions and allocated marks are indicated in green.
Return to Question 2

Describe what is meant by an ordered binary tree .

In a ordered binary tree ,

•Left children of a parent node precede the parent node in sequence;(1 mark)

•Right children of a parent node succeed the parent node in sequence.(1 mark)

[2]

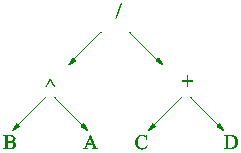
Given the arithmetic expression (B ^ A )/(C + D )

(i)Draw a tree structure diagram to represent the expression;[2 marks ]

The tree structure should appear as follows:

And one mark should be deducted for each incorrectly represented subtree. Note particularly the positions of A and B .

(ii)Convert the expression into Pre-fix notation;[2 marks ]

The Pre-fix expression should read

/ ^ B A +C D

And one mark should be deducted for each error. Note particularly the positions of A and B ,and the inclusion of the caret.

(iii)Convert the expression into Post-fix notation.[2 marks ]

The Post-fix expression should read:

B A ^ C D + /

And one mark should be deducted for each error. Note particularly the positions of A and B ,and the inclusion of the caret.

[6]

Given the following definition of a binary tree:

(i)Describe what is meant by an In-fix (In-order)traversal of a binary
tree.[2 marks ]

•The left subtree is traversed, followed by the node,(1 mark)

•and then the right subtree.(1 mark)

(ii)Write a recursive procedure, the signature of which is given below,which takes in a binary tree of the type given above, and performs an In-fix traversal of the tree. The procedure should print out the value stored at each node as it is traversed, and sum the value stored at each node, returning the sum as a reference parameter [5 marks ]

PROCEDURE InFixTraversalSum(root: BTreeNodePtr, VAR Sum:
INTEGER);

A sample definition of InFixTraversalSum follows:

PROCEDURE InFixTraversalSum(root: BTreeNodePtr, VAR Sum: INTEGER);
BEGIN
       IF(root ˆ.Left<> NULL) THEN
           InFixTraversalSum(root ˆ.Left, Sum);

       Write(root ˆ.Datum);
       Sum:= Sum+Datum;

       IF(root ˆ.Right<> NULL) THEN
           InFixTraversalSum(root ˆ.Right, Sum);
END;{ InFixTraversalSum }

The following marking scheme should be used:

•Testing nodes to see if they are leafs,before recursing;(1 mark)

•Recursing with the left subtree before performing any action;
(1 mark)

•Writing out the data after the left subtree recursion;(1 mark)

•And incrementing the Sum parameter;(1 mark)

•Then recursing with the right subtree.(1 mark)

[7]