| (a) |
Convert the number
|
[2] |
| (b) |
Calculate the value of the expression
(1 mark for converting correctly to a common base (any base will do), 1 mark for adding correctly in that base, 1 mark for correctly dividing, 1 mark for giving the result in BCD.)
|
[4] |
| (c) |
Explain how to add two integers in sign-modulus
format. •When the sign bits are the same, the magnitude of the result is the sum of the magnitudes of the arguments (1 mark); if this sum yields a carry then there is an overflow, otherwise the sign of the result is the same as the sign of the arguments (1 mark). •When the sign bits are different, the magnitude of the result is the difference between the magnitudes of the arguments (the larger magnitude less the smaller magnitude) (1 mark); the sign of the result is the same as the sign of the larger-magnitude argument (1 mark).
|
[5] |
| (d) |
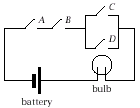
The switching circuit below controls a light bulb using four switches A, B, C, D.
Give a boolean expression in the switches
(using 1 to denote that the switch is conducting current) describing
the behaviour of the bulb.
|
[1] |
| (e) |
Simplify the expression
using the laws of boolean algebra. Identify
the laws used.
(3 marks for a complete correct calculation; failing that, 1 mark for each correct step to a maximum of 2 marks. Final 1 mark for a reasonable attempt at identifying the laws.)
|
[4] |
| (f) |
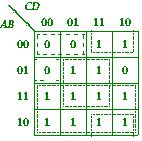
Find the simplified sum-of-product and product-of-sum forms of the function
by constructing a Karnaugh map.
The 1s are grouped with dots and the 0s with dashes — note that two groupings wrap around (1 mark for correct groupings ) , so the SOP form is A +BD +B'C (1 mark) and the POS form is (A +B +C)(A +B'+D) (1 mark).
|
[3] |
| (g) |
Find the prime implicants of the expression
using the Quine-McCluskey method.
so the four prime
implicants are
|
[4] |
| (h) |
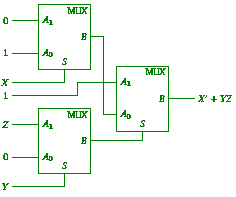
Implement NOT, AND and OR gates, each
using just one 2 ×1 multiplexor. Hence design a circuit for the expression
(1 mark each). They can be combined as follows to construct the circuit:
|
[4] |
| (i) |
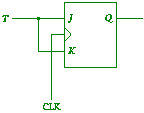
Give the excitation tables for a JK and
a T flip-flop, and show how to convert a JK flip-flop into a T flip-flop.
(1 mark each),and the conversion
(1 mark). |
[3] |
into
binary. 
(1
mark for the integer part, 1 mark for the fractional part.)
and express the result in BCD. 
(1
mark each).
using
just three 2 ×1 multiplexors. 
