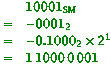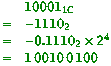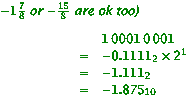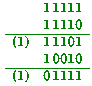December 1999
LD201 : LOGIC DESIGN

QUESTION 2

Total Marks: 15 Marks

• Question 1
• Question 3
• Question 4
• Question 5
• Cover Page

SUGGESTED SOLUTIONS
Solutions and allocated marks are indicated in green.
Return to Question 2

This question concerns a 9-bit floating point format, consisting of a 5-bit mantissa and a 4-bit exponent, both in two’s-complement format.

Give in decimal the largest and smallest positive and negative values that can be represented in this format in normalized form.

Range of floating-point format:
•The largest-magnitude positive normalized value is

•The smallest-magnitude positive normalized value is


(expressing this as the fraction is fine).
•The largest-magnitude negative normalized value is

•The smallest-magnitude negative normalized value is

(expressing this as the fraction is fine).
(1 mark each.)

Perform the following conversions:

(i) the sign-modulus integer represented by 10001 into this floating-point format, normalized;

Conversions:
(i) (1 mark; all or nothing)

(ii) the one’s-complement integer represented by 10001 into this floating-point format, normalized;

(ii) (1 mark; all or nothing)

(iii) the number represented in this floating-point format by 1 0001 0 001 into decimal.
(iii) (1 mark; answers

To add floating-point numbers, one must usually rescale to match exponents, before adding the mantissas and renormalizing the result.

(i) Rescale the two numbers with smaller exponents from part (b) to match the number with largest exponent. [2 marks]
Adding floating-point numbers:
(i) The largest exponent is 4, so we have
1 1000 0 001 ->1 1111 0 100
1 0001 0 001 ->1 1110 0 100
(1 mark each).

(ii) Add the three mantissas. (Hint: add any two, then add the third to the sum.) [1 mark]
(ii)
(All or nothing.) [1 mark]

(iii) What can you say about the result of adding the three mantissas? [2 marks]
(iii) The mantissa overflows; the sum of -1, -2 and -14 is -17, which is too large for signed 5 bits (1 mark). However, the result of the floating-point addition is still within the range of the floating-point format (1 mark).

What can you do to rectify the problem identified above, without changing the floating-point format?
Some values should be rescaled to prevent overflow (1 mark). For example, the intermediate result and the third number could be rescaled, so that instead of adding 1 1101 0 100 and 1 0010 0 100, the exponent should be increased and the mantissas shifted to 1 1110 0 101 and 1 1001 0 101. Then the addition proceeds as normal to (1) 1 0111 0 101 = (1 mark). Notice that this entails a loss of precision (1 mark).