|
(a)If it is known that
students = {john, mary}
subjects = {co230, ca208}
and
. 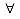 X:students
pass(X,co230) X:students
pass(X,co230)
then we can deduce the following additional fact
pass(john,co230) 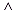 pass(mary,co230) pass(mary,co230)
(i)For each of the following statements,state what additional facts
ay be deduced:
•~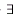 X:students
pass(X,ca208)[1mark ] X:students
pass(X,ca208)[1mark ]
~pass(john,ca208) 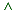 ~pass(mary,ca208)(1) ~pass(mary,ca208)(1)
•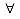 X:students X:students
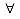 Y:subjects
pass(X,Y) [1mark ] Y:subjects
pass(X,Y) [1mark ]
[pass(john,co230)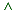 pass(mary,co230)
pass(mary,co230) 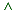 pass(john,ca208) pass(john,ca208)
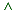 pass(mary,ca208)]
(1) pass(mary,ca208)]
(1)
•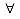 X:students X:students
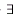 Y:subjects
pass(X,Y) [1mark ] Y:subjects
pass(X,Y) [1mark ]
[pass(john,co230) v pass(john,ca208)]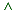 [pass(mary,co230)
v pass(mary,ca208)](1) [pass(mary,co230)
v pass(mary,ca208)](1)
•~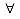 X:subjects
pass(john,X) [1mark ] X:subjects
pass(john,X) [1mark ]
~[pass(john,c0230) v pass(john,ca208)]OR
~pass(john,c0230) v~pass(john, ca208)(1)
(ii)Restate the following facts as quantified predicate expressions.
•~pass(john,ca208) 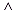 .~pass(john,co230)
[1mark ] .~pass(john,co230)
[1mark ]
. X:subjects
~pass(john,X)OR ~ X:subjects
~pass(john,X)OR ~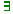 X:subjects
pass(john,X)(1) X:subjects
pass(john,X)(1)
•[pass(john,ca208) 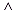 pass(john,co230)]
v[pass(mary,ca208) pass(john,co230)]
v[pass(mary,ca208) 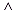 pass(mary,
co230)] [1mark ] pass(mary,
co230)] [1mark ]
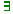 X:students X:students
 Y:subjects
pass(X,Y)(1) Y:subjects
pass(X,Y)(1)
•pass(john,ca208) v pass(mary,ca208) [1mark ]
.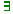 X:students
pass(X,ca208)(1) X:students
pass(X,ca208)(1)
(b)Use the following predicates to answer
this part of the question.
taught_by(X,Y) X
is taughtbyY
teach_subject(X,Y) X
teaches the subject Y
pass(X,Y) X
passes the subject Y
(i)Restate the following expression as an English sentence:
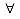 X X
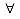 Y
[taught_by(X, mark) Y
[taught_by(X, mark) 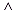 teach_subject(mark,Y)]
=>pass(X, Y) teach_subject(mark,Y)]
=>pass(X, Y)
[2marks ]
If a tudent is taught by Mark(1),then the
tudent passes all the ubject that Mark teaches (1).
(ii)Given that a student Karyn failed WW221,explain in English what
can be
concluded.You should use the given expression
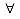 X X
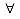 Y
[taught_by(X, mark) Y
[taught_by(X, mark) 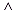 teach_subject(mark,Y)]
=> pass(X, Y) teach_subject(mark,Y)]
=> pass(X, Y)
and show clearly all your working and the logical rules used.[4 arks
]
(1)[taught_by(X,mark) 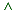 teach_subject(mark,Y)]=>pass(X,Y) teach_subject(mark,Y)]=>pass(X,Y)
(2) ~pass(karyn,ww221)
Substituting karyn for X and ww221 for Y
in (1),
(3)[taught_by(karyn,mark)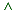 teach_subject(mark,ww221)]=>pass(karyn,ww221) teach_subject(mark,ww221)]=>pass(karyn,ww221)
Using contrapositive on (3),
(4) ~pass(karyn,ww221) =>[taught by(karyn,mark) 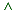 teach_subject(mark,ww221)] teach_subject(mark,ww221)]
Using Modu Ponen on (2),(4),we can conclude that
~[taught_by(karyn,mark) 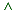 ~teach_subject(mark,ww221)] ~teach_subject(mark,ww221)]
=> taugh_ by(karyn,mark) 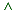 ~teach
subject(mark,ww221)(De Morgan ’s) ~teach
subject(mark,ww221)(De Morgan ’s)
Conclusion:Karyn wa not taught by Mark,or Mark did not teach WW221
(Alternative:some working may use Modus Tollens instead).(1)for correct
indication of substitution of variables,(2)for working,(1)for the
conclusion.
(iii)Given
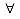 X X
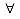 Y
[taught_by(X, mark) Y
[taught_by(X, mark) 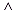 teach_subject(mark,Y)]
=>pass(X, Y) teach_subject(mark,Y)]
=>pass(X, Y)
and the knowledge that Joe passed WW221,explain if we can confidently
conclude that Mark teaches WW221 and that Joe was taught by Mark.[2
marks ]
The form of reasoning that would allow u
to make the conclusion is abductive reasoning.Given that the conclusion
is true,it may be because the premises are true,but it may not nece
arily be o (1).So we cannot confidently say that mark teaches WW221
and that Joe was taught by Mark. Joe might have been taught by another
lecturer teaching WW221 (1).
|