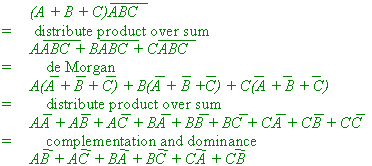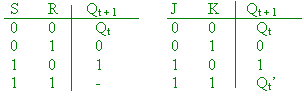April 2000
LD201 : LOGIC DESIGN

QUESTION 1 (Compulsory)

Total Marks: 30 Marks

• Question 2
• Question 3
• Question 4
• Question 5
• Cover Page

SUGGESTED SOLUTIONS
Solutions and allocated marks are indicated in green.
Return to Question 1

(a) Convert the number 30.125₁₀ into binary. [2 marks]
30.125₁₀ = 11110.001₂. (1 mark for the integer part, 1 mark for the fractional part) [2 marks]

(b) Calculate the value of the expression

and express the result in binary-coded decimal. [4 marks]
Converting everything to hexadecimal first, we have

(1 mark for converting everything correctly to a common base --- any base will do. 1 mark for correctly performing the addition. 1 mark for correctly performing the division. 1 mark for expressing the result in BCD.) [4 marks]

(c) Using the laws of boolean algebra, transform the expression

into a sum of products in the simplest form possible. Identify the laws used. [5 marks]
Simplification using boolean laws:

(3 marks for a completely correct calculation to a sum of products, or failing complete correctness, 1 mark for each correct step to a maximum of 2 marks. 1 mark for getting the simplest possible form above. Final 1 mark for a reasonable attempt at identifying the laws used.) [5 marks]

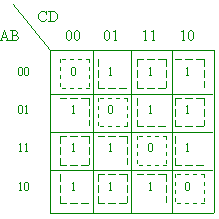
(d) Find the simplified sum-of-product and product-of-sum forms of the function

The 1s are grouped with dots and the 0s with dashes – note that two groupings wrap around (1 mark for correct grouping of 1s, 1 mark for 0s), so the SOP form is

AC’ + A’C + BD’ + B’D (1 mark) and the POS form is

(A + B + C + D)(A + B’ + C + D’)(A’ + B + C’ + D)(A’ + B’ + C’ + D’) (1 mark).

[4 marks]

(e)Find the prime implicants of the expression

using the Quine-McCluskey method. [5 marks
Quine-McCluskey:

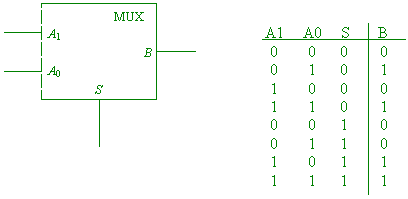
(1 mark for general layout of working), so the four prime implicants are m₁m_3, m₂m_3, m₁m_9, m₈m₉ (1 mark for each implicant). [5 marks]

(f) Draw a block diagram showing the connections on a 2 x 1 multiplexor, and give the truth table describing its behavior. Hence, show how to implement exclusive-or and exclusive-nor (that is, equality) using just two 2 x 1 mulitplexors each. [6 marks]
Here is the block diagram of a 2 ´ 1 multiplexor, and a truth table characterizing its behavior:

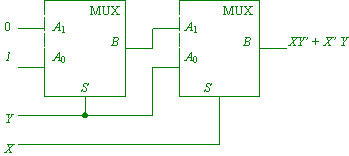
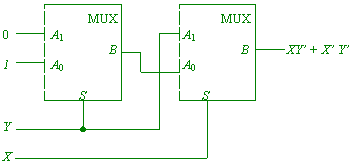
(1 mark each). Two such multiplexors can implement exclusive-or like this:

(1 mark for connections, 1 mark for labeling) and an equality-tester like this:

(1 mark for connections, 1 mark for labeling; maximum of 1 mark for using a third multiplexor to invert the output of the exclusive-or, thereby requiring three rather than two multiplexors.)

[6 marks]

(g) Give the excitation tables for an SR and a JK flip-flop, and show how to convert an SR flip-flop into a JK flip-flop. [4 marks)
The excitation tables are:

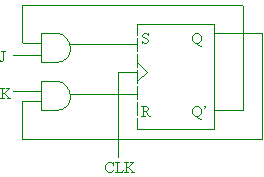
(1 mark each), and the conversion

(1 mark for connections, 1 mark for labeling). [4 marks)