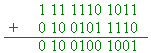|
This question concerns a 16-bit floating-point format, with an 11-bit mantissa in two’s-complement format and a 5-bit exponents in sign-modulus format. (a) What are the largest
and smallest positive and negative values that can be represented
normalized in this format? [4 marks]
(1 mark each) [4 marks]
(b) Express the numbers
–0.1238 and 4.5678 in normal form in this format.. [4
marks]
The number 4.5678:
(in each case, 1 mark for a numerically correct answer, and 1 mark for it being in normal form. It is ok if they truncate instead of rounding the second number.)
(c) Hence add these
two values, and express the result as a decimal fraction. [4 marks]
(1
mark) yielding a sum of (d) The IEEE 754 standard for floating point reserves some bit patterns for representing certain special values, apart from the patterns used to represent ‘normal’ values. Explain how each of the following special values might arise in floating point arithmetic: (i) positive infinity; (ii) negative infinity; (iii) ‘not a number’. [3 marks] Special values in IEEE 754: (i) dividing a positive value by zero (1 mark); (ii) dividing a negative value by zero (1 mark; if either this answer or the previous one is just ‘division by zero’, award a maximum of 1 mark for the two together); (iii) some other erroneous operation (1 mark), such as computing the square root of -1. [3 marks] |
(1
mark). Now the mantissae may be added:
or
4.4448 (1 mark). As a fraction ,this is 44448/83
= 234010/51210 = 58510/12810
(1 mark for either of the last two). [4 marks]