April 2000
LD201 : LOGIC DESIGN

QUESTION 4

Total Marks: 15 Marks

• Question 1
• Question 2
• Question 3
• Question 5
• Cover Page

SUGGESTED SOLUTIONS
Solutions and allocated marks are indicated in green.
Return to Question 4

(a) Describe two ways of using an n-bit two’s-complement parallel adder to perform n-bit subtraction. [3 marks]
Subtracting a number is the same as adding the negative of that number, so to compute x – y we could negate y then perform the addition x + (-y) (1 mark). More efficiently, we could compute the one’s-complement of y (obtained by inverting every bit) (1 mark) then perform the addition x + + 1, the extra 1 coming by setting the carry in (1 mark); this works because –y = + 1. [3 marks]

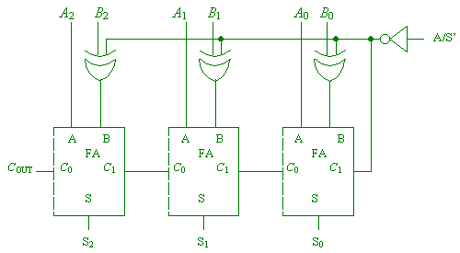
(b) Design a circuit to perform addition and subtraction of 3-bit two’s-complement numbers. Used XOR gates, and have a control input A/S’. Label your circuit design clearly. [4 marks]
3-bit parallel adder/subtracter:

(1 mark for chaining together the full adders, 1 mark for connecting the B inputs via XOR gates, 1 mark for correctly connecting the A/S’ control to the XOR gates and the carry-in; 1 mark for labeling and clarity.) [4 marks]

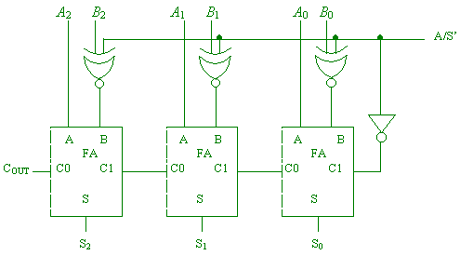
(c) Redesign the above circuit to use XNOR gates instead of XOR gates. [4 marks]
3-bit parallel adder/subtracter using XNOR:

(1 mark for chaining together the full adder, 1 mark for connecting the B inputs via XNOR gates, 1 mark for correctly connecting the A/S’ control to the XNOR gates and the carry-in; 1 mark for labeling and clarity.) [4 marks]

(d) Explain how to detect overflow in addition and subtraction of two’s-complement numbers. In each, give an expression characterizing overflow in terms of the signs S_A, S_B of the arguments, the sign S_C of the result, and the carry out C. [4 marks]

For addition, there is an overflow when the two arguments have the same sign and the sum has the opposite sign (1 mark). Overflow is thus characterized by

S_AS_BS’_C + S’_AS’_BS_C (1 mark). For subtraction, there is an overflow when the two arguments have different signs and the carry out is different from the sign of the difference (1 mark). Overflow is thus characterized by (S_AS’_B + S’_AS_B)(S_CC’ + S’_CC) (1mark). [4 marks]