April 1999
AP207: ADVANCED PROGRAMMING TECHNIQUES

QUESTION 4

Total Marks: 20 Marks

 Click here to access other questions

GRADE A
Sample student's solutions are indicated in green.
Return to Question 4

 
(a) (i) Describe what is meant by a binary tree. [2]
A binary tree is a hierarchical tree structure where each child node, except one (parent or root), is connected to exactly one parent node.

 
(ii) Explain the difference between a binary tree and an N-ary tree. [1]
In a binary tree, each parent node can have at least 2 child nodes or less. For N-ary tree, it can have more than one or many child nodes, that is, n child nodes.

 
(iii) Write a declaration for a suitable type to represent a (dynamic) binary tree, which contains an Integer at each node. [3]
Type
     TreeType = ^ TreeNode;
     TreeNode = RECORD
             info = integer;
             left = TreeType;
             right = TreeType;
         end;

  

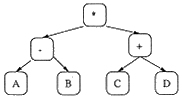
(b) Assume the following arithmetic expressions:
  • (A - B) * (C + D)
  • A * B + C

 
(i) Draw a tree structure diagram for each expression. [2]
pic1.gif (2892 bytes)

 

pic2.gif (2531 bytes)

 
(ii) Convert each expression into Pre-fix notation. [2]
(A - B) * (C + D)
Prefix : * - A B + C D

A * B + C
Prefix : + * A B C

 
(iii) Convert each expression into Post-fix notation. [2]
(A - B) * (C + D)
Postfix :  A B - C D + *

A * B + C
Postfix :  A B * C +

 
(c) (i) Write a recursive procedure - the prototype for which is given below - which takes the root of the binary tree above, and will perform a preorder traversal printing out the contents of each node as it traverses the tree. The nodes are of type Integer.

PROCEDURE PreOrderTraverser(Tree : TreeType);

 [4]
Procedure PreOrderTraverser ( Tree : TreeType);
Begin
    if (tree<>Nil) then
        begin
              writeIn(tree^.info);
              PreOrderTraverser ( tree^.left);
              PreOrderTraverser (tree^.right);
        end;
end;

 
(ii) Write a recursive function, the prototype for which is given below, which will take the root of the binary tree above, and count the number of nodes in the tree by performing a postorder traversal

FUNCTION PostOrderTraverser(Tree : TreeType) : Integer;

 [4]
function PostOrderTraverser(Type : TreeType) : Integer;
  Begin
    If (tree<>Nil) then
        PostOrderTraverser : = PostOrderTraverser ( tree^left) +       
        PostOrderTraverser(tree^.right)+1
   else
      PostOrderTraverser :=0;
end;