| (a) | Explain what it means when we say that | |
| (i) Events A and B are dependent. | [1] | |
| Events A and B are
dependent of the occurrence of one of the events affects the probability of the other
event in occurring.
|
||
| (ii) Events A and B are independent. | [1] | |
| Events A and B are
independent when the occurence of one event does not affect the occurence of the other
event.
|
||
| (b) | Let P(A), P(B), and P(A B)
be the probabilities of events A, B, and AB
happening. Give mathematical relationships relating each of these three probabilities (to
each other) for each of the following cases: |
|
| (i) Events A and B are dependent, | [1] | |
| Events A and B are
dependent: P(A|B) = P(A Ç B) / P(B)
|
||
| (ii) Events A and B are independent, and | [1] | |
| Events A and B are
independent: P(A Ç B) = P(A) * P(B)
|
||
| (iii) Events A and B are mutually exclusive. | [1] | |
| Events A and B are
mutually exclusive : P(A Ç B) = f
|
||
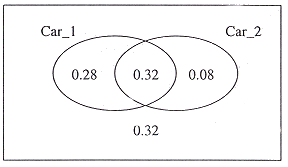
| (c) | During winter in Scotland, Mr Nettawa experiences difficulty in starting his two cars. The probability that the first car starts is 0.6, and the probability that the second car starts is 0.4. There is the probability of 0.32 that both cars start. | |
| (i) Are these events (i.e. that each of the cars starts) independent? Explain your answer. | [2] | |
| P(1st car starts ) =
0.6 P(2nd car starts ) = 0.4 P(both cars starts) = 0.32 If events are
independent, then probability of both cars start is But given P(both car starts) = 0.32 is not equal to 0.24, therefore the events are not independent.
|
||
| (ii) What is the probability that the first car starts but the second car doesn't? | [1] | |
| P (1st car starts and
2nd car doesn't) = P (1st car starts) - P (both car starts) = 0.6 - 0.32 = 0.28
|
||
| (iii) What is th probability that the second car starts but the first car doesn't? | [1] | |
| P (2ndt car starts and
1st car doesn't) = P (2nd car starts) - P(1st car doesn't) = 0.4- 0.32 = 0.08
|
||
| (iv) What is the probability that at least car starts? | [1] | |
| P (at least ocars
starts ) = P (1st car car starts) + P(2nd car starts) - P (both cars starts) = 0.6+0.4 - 0.32 = 0.68
|
||
| (v) What is the probability that neither car starts? | [1] | |
| P(neither car starts) = 1 - 0.68 = 0.32
|
||
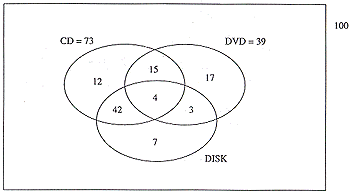
| (d) | A computer manufacturer has undertaken a survey of 100 businesses to determine which of the three types of external memory devices they commonly use: CD, DVD or diskette. A total of 39 businesses uses DVD, whilst 73 businesses made use of CD, 12 businesses used CD only, whilst 17 used only DVD, 42 businesses used both CD and diskette, but not DVD. Only 4 businesses used all three devices; all of the businesses used at least one of the devices. | |
| (i) Draw a Venn diagram to represent the results of the survey. | [5] | |
|
||
| (ii) How many businesses used CD and DVD, but not diskettes? | [1] | |
| 15 businesses use CD
and DVD but not diskette.
|
||
| (iii) How many businesses used DVD and diskettes, but not CD? | [1] | |
| 3 businesses use DVD and diskette, but not CD. | ||
| (iv) What is the probability that a firm that uses diskettes does not use CDs? | [2] | |
| 42 + 2 + 3 + 7 = 56 P(uses diskette does not use CDs) = 10/56
|
