April 1999
QT211: QUANTITATIVE ANALYSIS FOR MANAGEMENT

QUESTION 4

Total Marks: 20 Marks

 Click here to access other questions

GRADE A
Sample student's solutions are indicated in green.
Return to Question 4

 
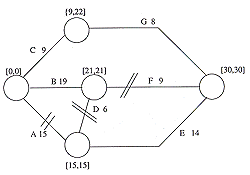
The information given below relates to a construction project for which your company is about to sign a contract. Seven activities are necessary and the normal duration, normal cost, crash duration and crash cost have been derived from the best available sources. Each activity may be reduced to the crash duration in weekly stages at a pro-rated cost. This project incurs a fixed cost of $500 per week.
 
Activity Immediate Predecessors Normal Time Crash Time Normal Cost Crash Cost
A - 15 12 4500 5250
B - 19 14 4000 4500
C - 9 5 2500 4500
D A 6 5 1700 1940
E A 14 9 4300 5350
F B,D 9 6 2600 3440
G C 8 3 1800 3400

 
(a) Draw the network diagram for the above project using the normal times for the activities involved. [5]

pic2.gif (5070 bytes)

 
(b) What are the critical path activities for the project? What is the expected project completion duration and cost? [4]
Critical path is A ® D ® F
Expected project completion is 30 weeks
Total cost = $21, 400 + 30 ( 500)
                = $ 36, 400

 
(c) Assume that the company wishes to complete the project in 26 weeks.
(i) Write down the time each path would take without crashing. [3]
A ® E   29 weeks
A ®  D ® F        30 weeks  * critical
B ® F    28 weeks
C ® G   17 weeks

    

(ii) Copy and complete the following table: [3]
 
Activity Possible Saving (weeks) Additional Cost ($) Additional Cost per Week
A 3 750 250
B 5 500 100
C 4 2000 500
D 1 240 240
E 5 1050 210
F 3 840 280
G 5 1600 320

 
(iii) Use the table to justify what crashing decisions you would recommend in order to meet the completion duration at the least possible cost.
Show your working clearly.		 [5]
Step 1 :
A ® E    29 weeks
A ®  D ® F        30 weeks  * critical
B ® F    28 weeks
C ® G   17 weeks

Looking at the critical path, it is cheapest to crash D by 1 week.
Savings = 500 - 240 = $260

Step 2:
A ® E    29 weeks  * critical
A ®  D ® F        29 weeks  * critical
B ® F    28 weeks
C ® G   17 weeks

Looking at the critical path, it is only possible to crash a
Savings = 500 - 250 = $250

Step 3:
A ® E    28 weeks
A ®  D ® F        28 weeks  * critical
B ® F    28 weeks    *critical
C ® G   17 weeks

(option 1 )
Crashing A and B by 2 days gives savings of = $1000 - (500-200)
                                                                       = $ 300
(option 2)
Crashing E and F by 2 days gives savings of = $1000 - (420 + 560)
                                                                      = $20

therefore, it is better to crash A and B.

Final chart:
A ® E    26 weeks
A ®  D ® F        26 weeks  * critical
B ® F    26 weeks    *critical
C ® G   17 weeks

Total cost of new project = $35, 590
Therefore, there is a new reduce in cost.