|
(a) Deductive reasoning is based on Modus
Ponens. Write down the symbolic
expression for Modus Ponens and explain it. [2]
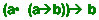 [1] [1]
Given that the antecedent and the rule are true, we can infer that
the
consequent is also true. [1]
(b) In abductive reasoning, given that
the symbolic rule “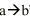 ”
and the consequent “b” are true, we can infer that the antecedent
“a” is true. Using an example, briefly describe a problem
when such a reasoning approach is used. [3] ”
and the consequent “b” are true, we can infer that the antecedent
“a” is true. Using an example, briefly describe a problem
when such a reasoning approach is used. [3]
In the example “If it is raining, then
the grass is wet”, represented as
 ,
given that the grass is wet and using abductive reasoning, ,
given that the grass is wet and using abductive reasoning,
we can conclude that it is raining. While one of the possible causes
of
grass to be wet is rain, there are other possible causes, like morning
dew or the gardener watering the grass. Therefore, it is not safe
to make such a conclusion. [1 mark for example, 2 marks for a good
explanation]
(c) Given the following predicates:
study_hard(X,Y)
pass_event(X,Y)
awarded(X,Y) |
X studies hard for event Y
X passes event Y
X is awarded Y |
(i) Represent the following statements
as predicate expressions [2]
If a person studies hard, then he passes the examinations.
A person is awarded a diploma if he passes the examinations.
(ii) Given the truth of the two statements above, a reasoning technique
allows us to infer the award of a diploma to John from the fact that
he
worked hard. Name the reasoning technique and write down the
symbolic representation of this reasoning technique. [3]

(d) Given the following predicates:
father(X,Y)
spouse(X,Y)
|
X is the father of Y
X is married to Y |
And facts:
father(tom,mary)
father(tom, mike)
father(george, tom)
spouse(tom, tina)
(i) Using only the predicates given above, define a rule for
grandfather(X,Y) such that X is the grandfather of Y. [1]
(ii) State the values of Y such that grandfather(george, Y) is true.
[2]
(iii) Using only the predicates given above, define a rule mother(X,Y)
such
that X is the mother of Y. State and explain any assumptions that
you
make that will ensure that your rule is valid. [2]

|

