|
(a) Traditional logic is binary in nature.
With the aid of an example, briefly
describe two reasons why this form of logic is insufficient. [3]
Binary logic has only two values true or
false. However, there are many situations for which the answer is
not strictly true or false. [1] Fuzzy logic allows truth values to
be represented in terms of degrees. [1] plus [1] for an appropriate
example.
(b) Given the following fuzzy set:
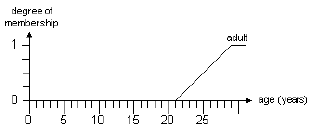
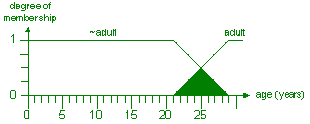
(i) Show in the diagram the complement operation on the adult fuzzy
set
and give an appropriate name for the resulting fuzzy set. [2]
(ii) Show in a diagram the intersection operation of the adult fuzzy
set and
adult complement fuzzy set. [1]
(iii) If a person is 23 years old, what are the membership values
of the person
in the adult fuzzy set and in the adult complement fuzzy set? [2]
(i) Appropriate name: ~adult or child. [1]
Solution diagram: [1]
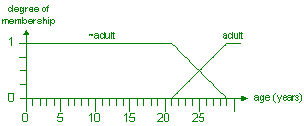
(ii) Solution diagram: [1]
(iii) 0.25 and 0.75 [2]
(c) Given the following fuzzy sets:
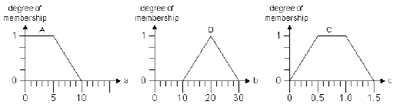
(i) Briefly describe the steps in single rule fuzzy inference. [3]
(ii) Given that  ,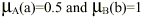
what are the values of a and b. [2]
(iii) Given the fuzzy rule “If fuzzy set A and fuzzy set B then
fuzzy set C,
 ,
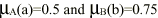show the output fuzzy set in the diagram.
What is the value of c in the output fuzzy set? [2]
(i) Fuzzification: Finding the membership
values for the
corresponding input in each fuzzy set. [1]
Inference: From the membership value find the output fuzzy set for
each rule. [1]
Defuzzification: From the output fuzzy set, find the final output
value. [1]
(ii) a = 7.5, b=20 [2]
(iii) 0.75 [1]
Solution diagram: [1]
|
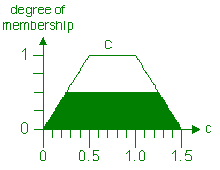