|
A. Number System (5)
(a) Convert the number 40.12510 into Binary. [2]
(b) Add together the different
number systems, ( 38 + E0416 ) and give the
answer in BCD. [3]
B. Logic Representation. (3)
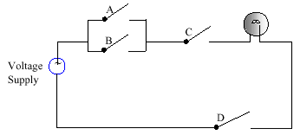
(c) Find the Boolean expression for the switching circuit below. [1]
(d) Let p be statement ‘Tom speaks English’, and
q the statement ‘Tom speaks
French’. Represent the statements below using Boolean logic,
in terms of p and
q.
“Tom speaks neither English nor French” [1]
(e) Represent the above question (d) using one Logic gate. [1]C. Boolean
Algebra. (12)
(f) Using Boolean algebra and de Morgan’s Law or otherwise prove
the property
below. [4]
A’B+AB’=[(A{AB}’)’(B{AB}’)’]’
(g) By constructing the Karnaugh Map for the function
F(A,B,C,D) = 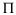 ( 0,1,5,13) + don’t care
( 0,1,5,13) + don’t care 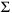 (4,14) (4,14)
find the ‘sum of products’ and ‘product of sums’.
[4]
(h) Solve the following using Quine McClusky
the expression,
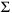 (
m0,m2, m3 m8, m9,m14,m15) (
m0,m2, m3 m8, m9,m14,m15)
up to the prime implicants. Indicate the prime implicants clearly.
[4]
D. Sequential Circuits (8)
(i) Give the Characteristic table of a JK flip-flop and convert an
SR to a JK flip-flop.
[4]
(j) A binary cell has the following connections: [4]
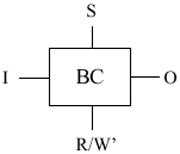
The cell acts as a single bit memory.
Its behaviour is as follows: if select
control S is low, the bit remains unchanged and the output is zero:
if S is high
and the read / write control R/W’ is high, the bit remains unchanged
and the
output O is the same as the bit; if S is high and R/W’ is low,
the bit is replaced
with the input I and the output is zero.
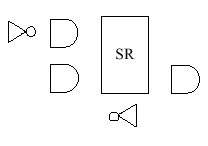
Design an implementation of such a cell. Hint: one implementation
can be
constructed by appropriately connecting the following components.
E. Theory (2)
(k) Explain what is meant by the term semiconductor. [2]
|