|
((a) Let G be a graph. Prove that the
sum of the degrees of the vertices of G is equal to twice the number
of its edges. [2]
(a) Each edge will be attached to exactly two vertices. So adding
each edge increases the sum of the degrees of the vertices by two.
Therefore, sum of degrees of vertices equals twice the number of edges.
[2]
(b) Calculate the number of edges of
each of the following graphs, if the graph
exists. For graphs that do not exist, explain their non-existence.
(i) G1: A 5-regular graph with 7 vertices. [1]
(ii) G2: The complete bipartite graph K2,4. [1]
(iii) G3: The complete graph K5 with 5 vertices. [1]
(b) (i) Sum of degrees of vertices of G1 is 5 × 7 = 35. So number
of edges is 17.5, so graph cannot exist. [1]
(ii) Number of edges = 2 × 4 = 8. [1]
(iii) Number of edges = 5 × 4/2 = 10. [1]
(c) For the graphs that do exist:
(i) Draw the graphs, labelling all vertices [4]
(ii) Write down their adjacency matrices and their distance matrices.
[6]
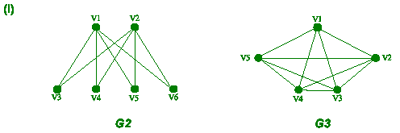
Two marks for each [4]
(ii)

|

