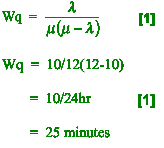|
(a) Carlton Savings and Loan has one
drive-in service window. The arrival of cars
occurs at a mean rate of 10 cars per hour. The mean service rate is
12 cars per
hour.
Use this information to answer the problems that follow. Work to 2
decimal
places.
(i) What is the probability that the service facility is idle? [2]
(i) 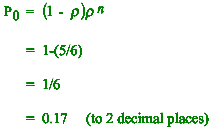 [2] [2]
(ii) What is the average number of cars in the system? [2]
(ii)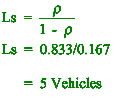 [2]
[2]
(iii) What is the probability that there are at least two cars in
the system? [2]
(iii) P(2 or more vehicles in system) [1]
= p**2
= (0.833**2) [1]
= 0.69 (to 2 decimal places [1]
(iv) How long, on average, would a customer have to wait before being
attended to? Give your answer in minutes. [2]
(iv)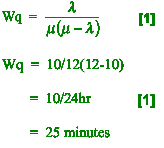
(b) Discuss the tradeoff between the
cost of increasing service capacity and the cost of keeping customers
waiting. [3]
(b) Increasing the service capacity, for
example by opening more counters, causes operational costs to increase.
If customers are kept waiting, they may choose to go elsewhere. [2]
A balance must be reached so that the operation is profitable and
customers are satisfied. [1]
(c) If the arrival rate of a single-channel
queuing system is halved, will the average
time a unit spends waiting for service halve? Justify your answer.
[4]
(c) Average time a unit spends in queue waiting
for service is given by
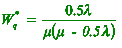
Halving the arrival rate gives a new average time a unit spends in
queue
waiting for service:
As 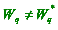 , the average time spent waiting for service does not halve. [2]
, the average time spent waiting for service does not halve. [2]
|
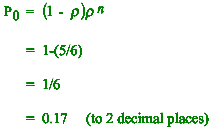 [2]
[2]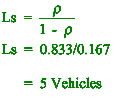 [2]
[2]