|
(a) On his way to catch
a bus to work each morning, Mr Adams will sometimes buy a newspaper,
and will sometimes buy a sandwich. The probability that he buys a
newspaper is 0.5, and the probability that he buys a sandwich is 0.3.
Buying a newspaper and buying a sandwich are independent events. The
probability that Mr Adams misses his bus is 0.1. However, if he buys
a newspaper this may delay him, and so on days when he buys a newspaper
the probability that he misses his bus is 0.15.
(i) Calculate the probability that Mr Adams buys a newspaper and buys
a
sandwich. [2]
(ii) Calculate the probability that Mr Adams buys a newspaper or buys
a
sandwich. [2]
(iii) Calculate the probability that Mr Adams misses the bus and buys
a
newspaper. [3]
(iv) Calculate the probability that Mr Adams has bought a newspaper
if he
has missed the bus. [3]
(a) Let: N be the event that Mr Adam buys
a newspaper; S be the event that Mr Adams buys a sandwich; and M be
the event that Mr Adams misses
the bus.
(i) P(N and S) = P(N)P(S) = 0.5 x 0.3 = 0.15 [2]
(ii) P(N or S) = P(N)+P(S) - P(N and S) = 0.65 [2]
(iii) P(M and N) = P(M\N)P(N) = 0.15 × 0.5 = 0.075 [3]
(iv) P(N\M) = P(M and N)/P(M) = 0.75 [3]
(b) (i) Give one advantage
and one disadvantage of using the expected value of
a probability distribution. [2]
(b) (i) Advantages of using the expected
value:
- Easy to understand, simple to calculate
- Represents the whole figure by a single number
- Arithmetically takes account of the expected variabilities of all
outcomes
Any one. [1]
Disadvantages of using the expected value:
- By representing the whole distribution with a single value it ignores
the range and skewness
- Makes the assumptions that the decision maker is risk neutral.
Any one. [1]
(ii) An ice cream vendor finds that sales of ice cream each day satisfy
the
following distribution:
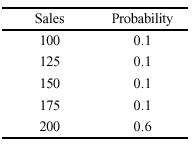
If each ice cream is sold for $2, calculate
the expected takings of the
vendor each day. [3]
(ii) Expected sales of ice creams. [2]
= 0.1 × 100 + 0.1 × 125 + 0.1 × 150 + 0.1 ×
175 + 0.6 × 200 = 175
So expected takings = $2 × 175 = $350. [1]
|
