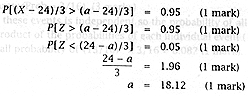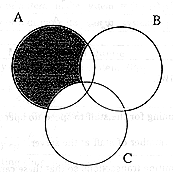| 1 |
(a) Will doubling the
service rate of a single-channel queuing system halve the average waiting time in the
queue? Give an explanation of your answer. |
[3] |
|
[Hint : Formulae relating to
queuing are provided]. |
|
|
From the
formulae sheet where m is the average waiting time and l the mean arrival rate: |
|
|
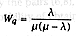
|
|
|
Doubling m gives a new waiting time 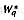 |
|
|

|
|
|
[2
marks] |
|
|
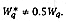 |
|
|
[1
mark] |
|
|
|
|
|
(b) The waiting time in queues may
be reduced by increasing the number of servers. Give two other ways in which the waiting
time might be reduced. |
[2] |
|
|
Conducting training
for the staff to speed up operations. |
|
|
|
Increase the number of
staff at the server. |
|
|
|
Automate routine
transactions so that these can be handled by machines. |
|
|
1 mark for
each point, maximum of 2 marks. |
|
|
[2
marks] |
|
|
|
|
|
(c) If the random variable X follows
a Normal distribution with a mean of 24 and a variance of 9 i.e. X ~ N(24,9), and
given that P(x > a) = 0.950, deduce the value of a. Explain
your answer carefully (you might find it helpful to draw a diagram). |
[5] |
|
Since P
(X > a) > 0.5, a must be less than the mean |
|
|
Standardising,
so that we can use tables of the Z ~ N (0,1) distribution, we have (using the
tables of the N (0,1) distribution), since P (X > a) = 0.95 |
|
|
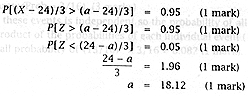
|
|
|
[5
marks] |
|
|
|
|
|
(d) Find the mean and standard
deviation of the following set of numbers: |
[5] |
|
2, 4, 8, 12, 5, 8, 10. |
|
|
Mean is 49
/ 7 = 7 |
[2] |
|
s.d. is 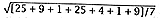 |
[2] |
|
= 3.25 |
[1] |
|
|
|
|
(e) Sketch the Venn Diagram for
the expression A - B - C. |
[2] |
|
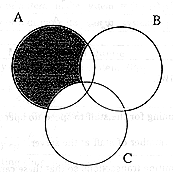
|
|
|
[2
marks] |
|
|
|
|
|
(f) Give three types of inventory
cost (note: purchasing cost may not be used as an answer). |
[3] |
|
|
Goodwill/stockout
costs |
[1] |
|
|
Carrying costs |
[1] |
|
|
Ordering costs |
[1] |