| 4. |
The Millennium Company wishes to
invent and market a new communication security software. Millennium has a choice of two
different research and development plans: Plan A and Plan B. |
|
|
|
Plan A costs $1 million and has a probability
of 0.4 of succeeding. |
|
|
|
Plan B costs $500,000 and has a probability of
0.3 of succeeding. |
|
|
In the event of success Millennium
has to decide whether to advertise the software aggressively or lightly. The software will
either obtain full or partial market acceptance. |
|
|
|
Aggressive advertising will cost $400,000 and
gives a probability of 0.7 of full acceptance of the software. |
|
|
|
Light advertising will cost $100,000 and gives
a probability of 0.5 of full acceptance of the software. |
|
|
Full market acceptance of the
software marketed is worth $4 million for Plan A, and $3 million for Plan B. Partial
market acceptance is worth $2 million for both Plan A and Plan B. |
|
|
|
|
|
|
|
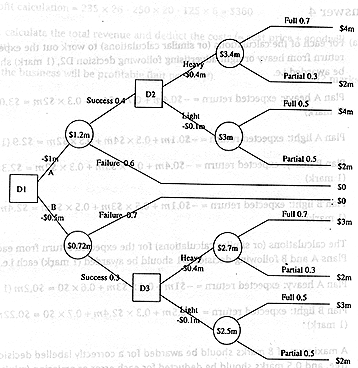
(a) Draw the decision tree showing all of the
possible decisions and outcomes, ensuring that you label your diagram clearly. Work out
the value of each decision node in the diagram. |
[14] |
|
|
For each of the
calculations (or similar calculations) to work out the expected return from heavy or light
advertising following decision D2, |
[1] |
|
|
should be awarded i.e. |
|
|
|
Plan A heavy: expected
return = -$0.4m + 0.7 X $4m + 0.3 X $2m = $3.0m |
[1] |
|
|
Plan A light: expected
return = -$0.1m + 0.5 X $4m + 0.5 X $2m = $2.9m |
[1] |
|
|
Plan B heavy: expected
return = -$0.4m + 0.7 X $3m + 0.3 X $2m = $2.3m |
[1] |
|
|
Plan B light: expected
return = -$0.1m + 0.5 X $3m + 0.5 X $2m = $2.4m |
[1] |
|
|
The calculations (or
similar calculations) for the expected return from each of Plans A and B following
decision D1 should be awarded |
[1] |
|
|
each i.e. |
|
|
|
Plan A heavy: expected
return = -$1m + 0.4 X $3m + 0.6 X $0 = $0.2m |
[1] |
|
|
Plan B light: expected
return = -$0.5m + 0.3 X $2.4m + 0.7 X $0 = $0.22m |
[1] |
|
|
A maximum of 8 marks
should be awarded for a correctly labelled decision tree, and 0.5 marks should be deducted
for each error or omission (minimum 0 marks). |
|
|
[14
marks] |
|
|
|
|
|
|
|
|
|
|
(b) Based on your analysis, explain clearly
which plan and which level of advertising Millennium should adopt. |
[3] |
|
|
Based on the decision
tree the highest expected return is given by choosing Plan B with light advertising,
giving a net EMV $0.22m. |
|
|
[3
marks] |
|
|
|
|
|
|
(c) Consider further the probability of
failure. If you were the managing director of Millennium would you undertake the
development of this software? Justify your answer. |
[3] |
|
|
Two possible answers. |
|
|
|
For plans A and B the
probability of failure is 60% and 70% respectively i.e. each plan has a greater chance of
failing than of succeeding. So, even though the analysis shows an expected profit, as a
cautious manager, I would not attempt to develop the software by either plan. |
|
|
|
Alternatively:
Although the probability of failure for both plans is high, we expect to make a profit
even allowing for this in the construction of the decision tree. Although the net EMV is
only $0.22m, if we were to adopt plan B with light advertising, and if it were to
be successful we would actually make a profit of $1.9m, on an outlay of 0.50m.
I consider this level of profit to be worth the increased risk, and I would therefore go
ahead with this plan. |
|
|
[3
marks] |
|
