| (a) | (i) How many different ways are there of choosing a group of 5 people from a group of 25? | [2] |
| (ii) How many different ways are there of choosing a group of 8 people from a group of 20? | [2] | |
| (iii) On a school field trip, the teacher
needs to divide a class of 25 children into three groups of 5, 8 and 12 respectively. How
many ways are there of doing this?
|
[3] | |
| (i) 25C5 = 53130 | ||
| (ii) 20C8 = 125970 | ||
| (iii) 25C5
x 25-5C8 x 25-5-8C12 = 53130 x 125970 x 1 =
6,692,786,100
|
||
| (b) | How many integers from 0 through 60 must you pick in order to be sure of getting at least one that is odd? Justify your answer. | [2] |
| 32 There are 61 integers between 0 and 60 inclusive. There are 31 non-odd integers; the 30 even integers and zero. Therefore 32 integers need to be picked to ensure that at least one add integer is picked.
|
||
| (c) | Three people have been exposed to a contagious disease. Once exposed, a person has an 60% chance of actually becoming ill. | |
| (i) What is the probability that exactly two
people become ill? (ii) What is the probability that at least two people become ill? (iii) What is the probability that none of the people become ill? |
[2] [2] [2] |
|
| (i) P(Exactly two
become ill) = 3 x (0.62 x 0.4) = 0.432
|
||
| (ii) 0.648 A possible method is given below. P(At least two become ill) = P(Exactly two become ill) + P(Exactly three become ill) = 0.432 + 0.63 = 0.432 + 0.216 = 0.648
|
||
| (iii) P(None of the
three people become ill) = 0.43 = 0.064
|
||
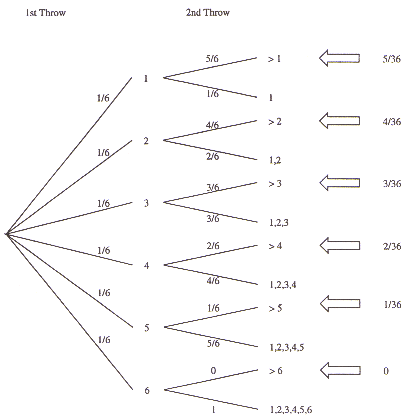
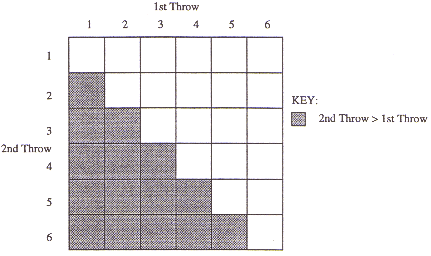
| (d) | A die is rolled twice. What is the probability
that the score on the second throw is greater than the score on the first throw? You must show your working.
|
[5] |
| Method one
P(2nd Throw > 1st Throw) = 5/36 + 4/36 + 3/36 + 2/36 + 1/36 = 5/12 Method 2
15 out of the 36 squares are shaded, so p(2nd Throw > 1st Throw) = 15/36 = 5/12 |