August 1999
MA214 : DISCRETE MATHEMATICS

QUESTION 3

Total Marks: 20 Marks

 Click here to access other questions

SUGGESTED SOLUTIONS
Solutions and allocated marks are indicated in green.
Return to Question 3
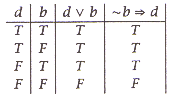
(a) (i) What does it mean for an argument to be valid?

(ii) Determine, by constructing a truth table, whether or not the following argument is valid.

My book is either on my desk or on the bookshelf.
It is not on the book shelf, therefore it must be on my desk.

(iii) Is the following statement a tautology or a contradiction?

(d Ú b) Þ (~b Þ d)

where we define our terms

b: my book on my bookshelf     d : my book is on the desk

Justify your answer.

 

 [2]

 

[4]

 

 

 

 

[3]
(i)
An argument is valid if the conclusion is true whenever all the premises are true.

 
(ii)

                pic9.gif (4030 bytes)

 
(iii)
It is tautology because it is always true.

 
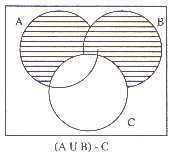
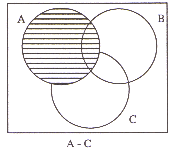
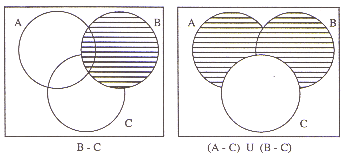
(b) Prove, using Venn diagrams that for all sets A, B and C

(A È B) - C º (A - C) È (B - C)

You must show your working

 

 [7]
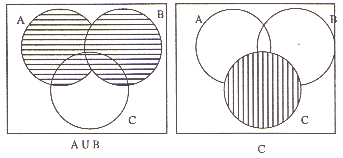
        pic10.gif (13055 bytes)

        pic10a.gif (6346 bytes)pic10b.gif (5401 bytes)

         pic10c.gif (11242 bytes)

 
(c) Let S be the statement

" x Î R if x(x+1) > 0 then x > 0 or x < -1

(i) Write down the contapositive of S.

(ii) Write down the converse of S.

 

  

 

[2]

[2]
(i) " x Î R if -1 £  x £  0 then x(x + 1) £ 0

 
(ii) " x Î R if x > 0 or x < -1 then x(x + 1) > 0