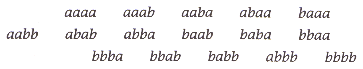| (a) | Define the function f : Z ® Z by the rule f (n) = 2n, for all integers n. (i) What property must be true of a one-to-one function? (ii) What property must be true of an onto function? (iii) Is f one-to-one? Prove or give a counter example. (iv) If f onto? Prove or give a counter example.
|
[1] [1] [2] [2] |
| (i) A function g : A ® B is one to one if "x, y Î A, g(x) = g(y) implies x = y
|
||
| (ii) A function g : A ® B is onto if for each y Î B, $x Î A such that g(x) = y
|
||
| (iii) f is one to one. One mark f (n) = f(m)
|
||
| (iv) f is not onto. One mark No element maps onto 1 (or indeed any of the odd numbers). |
||
| (b) | Let S be the set {a,b}, and define S4 to be the set of all strings over of length 4. | |
| (i) List all sixteen elements of S4. The relation R is defined on S4 as follows: for all s, t Î S4, s Rt Û s has the same first two characters as t. (ii) Is aabb R aabb? (iii) Is abba R baab? (iv) Write down all the elements which are related to abba.
|
[3]
[1] [1] [2] |
|
| (i)
|
||
| (ii) Yes
|
||
| (iii) No
|
||
| (iv) abaa, abab, abba, abbb
|
||
| (c) | (i) What properties must be an equivalence
relation hold? (ii) D is the binary relation defined on R as follows: " x,y Î R, xDy Û xy ³ 0Is D an equivalence relation? Justify your answer.
|
[4]
[3] |
(i) A relation R : S « S is
A relation is an equivalence if it it reflexive, symmetric and transitive.
|
||
| (ii) D is not an equivalence relation since it is not transitive: (1, 0) Î D since 1 x 0 = 0 and 0 ³ 0 and (0, -1) Î D since 0 x -1 = 0 and 0 ³ 0 but (1, -1) Ï D since 1 x -1 = -1 and -1 < 0
|