The IT department of a large bank
has developed for a new database interrogation software. It now has three choices on
how to proceed in attempting to bring the product to market:
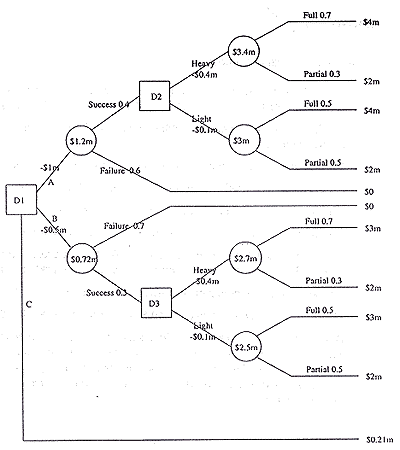
If the bank chooses either Plan A or Plan B it will develop the software itself. The bank has estimated that Plan A will cost $1 million and has probability of 0.4 of succeeding, and Plan B will cost $500,000 and has probability of 0.3 of succeeding. If the development process is successful, then for either Plan A or Plan B the bank's marketing department has to decide whether to advertise the software aggressively or lightly. The software will then either obtain full or partial market acceptance.
Full market acceptance of the software marketed is worth $4 million for Plan A, and $3 million for Plan B. Partial market acceptance is worth $2 million for both Plan A and Plan B.
|
||
| (a) | Draw the decision tree showing all
of the possible decisions and outcomes, ensuring that you label your diagram clearly. Work
out the value of each decision node in the diagram.
|
[15] |
| From each of
the calculations (or similar calculations ) to work out the expected return from heavy or
light advertising following decision D2, (1 mark) should be awarded i.e. For Plan C the return of $210,000 is guaranteed and the bank has no further involvement (1 mark). For Plan A heavy: expected return = -$0.4m + 0.7 x $4m + 0.3 x $2m = $3.0m (1 mark) For Plan A light: expected return = -$0.1m + 0.5 x $4m + 0.5 x $2m = $2.9 (1 mark) Plan B heavy: expected return = -$0.4m + 0.7 x $3m + 0.3 x $2m = $2.3m (1 mark). Plan B light: expected return = -$0.1m + 0.5 x $3m + 0.5 x $2m = $2.4m (1 mark) The calculations (or similar calculations) for the expected return from each of Plans A and B following decision D1 should be awarded (1 mark) each i.e. Plan A heavy: expected return = -$1m + 0.4 x $3m + 0.6 x $0 = $0.2m (1 mark) Plan B light: expected return = -$0.5m + 0.3 x $2.4m + 0.7 x $0 = $0.22m (1 mark) A maximum of 9 marks should be awarded for a correctly labelled decision tree. 1 mark should be deducted for each type or error or omision in labelling, and for each arithmetic error, but repeated similar error should only be penalised once (minimum 0 marks). Please take special care in the examiner's meeting to review this marking scheme appropriately.
|
||
| (b) | Based only on your analysis, explain clearly which plan the bank should adopt. | [2] |
| Based only
on the decision tree the highest expected return is given by choosing Plan B with light
advertising, giving a net EMV $0.22m.
|
||
| (c) | Consider further which choices are open to you. If you were the managing director of the bank, what would you choose to do? Justify your answer. | [3] |
| At least two
possible answers. Please award marks to any candidate who demonstrates an understanding of
the ideas of random chance and certainty in their answer. For plans A and B the probability of failure is 60% and 70% respectively i.e. each plan has a greater chance of failing than succeeding. So, even though the analysis shows an expected profit in excess of the amount offered by the contractor, as a cautious manager, I would not attempt to develop the software by either plan. I would instead choose plan C, which has a guaranteed return of $0.21m. Alternatively: Although the probability of failure for both plans A and B is high, we expected to make a profit even allowing for this in the construction of the decision tree. Although the net EMV is only $0.22m, if we were to adopt plan B with light advertising, and if it were to be successful we would actually make a profit of $1.9m on an outlay of $0.5m. I consider this level of profit to be worth the increased risk, and I would therefore go ahead with this plan. |