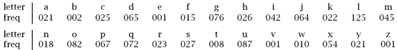December 1999
SC223 : COMPUTER SECURITY

QUESTION 2

Total Marks: 15 Marks

• Question 1
• Question 3
• Question 4
• Question 5
• Cover Page

SUGGESTED SOLUTIONS
Solutions and allocated marks are indicated in green.
Return to Question 2

What is a monoalphabetic substitution cipher?
In a monoalphabetic substitution cipher, each letter of the plaintext is replaced with a single letter of ciphertext (1 mark). The same mapping between plaintext and ciphertext is used for every letter of the plaintext (1 mark).

How does a polyalphabetic substitution cipher differ from a monoalphabetic one?
A polyalphabetic substitution cipher uses multiple mappings between plaintext and ciphertext, not just a single mapping. (The Study Guide implies that a polyalphabetic substitution cipher produces multiple characters for each letter of plaintext, rather than a single character generated from a varying mapping. This is incorrect, but should receive credit anyway.)

What is it that makes a polyalphabetic substitution cipher more secure than a monoalphabetic cipher?
A good polyalphabetic cipher will have a flat frequency distribution, whereas the monoalphabetic cipher will have the same shaped frequency distribution as the plaintext (1 mark); hence the monoalphabetic cipher reveals information about the substitution mapping that the polyalphabetic cipher hides (1 mark).

Explain the difference between a block cipher and a stream cipher. Which is the more secure?
A stream cipher encodes each letter as soon as it is input, whereas a block cipher encodes a whole block of letters at once (1 mark). A stream cipher is simpler and faster, but a block cipher is more secure (1 mark).

Explain how to decrypt a monoalphabetic substitution cipher.
To decrypt a monoalphabetic substitution cipher:

• compute the frequency distribution of the ciphertext (1 mark);

• compare with the (known or estimated) frequency distribution of plain text, and match uptoobtain a firstguessat themapping(1 mark);

• finding the complete mapping may take some trial and error, especially for infrequent letters, as the two distributions will probably not match precisely (1 mark);

• use can also be made of known or probable plaintexts (1 mark).

 Decrypt the following extract from a block of ciphertext.

nxlotpqyrgmld pd ksq

It is English text, encrypted using a monoalphabetic cipher. The complete ciphertext had the frequency distribution, in letters per thousand,

For reference, the frequency distribution of ordinary English text, also in letters per thousand, is

Show your working.

Sorting the letters of the alphabet according to their frequency in ordinary English yields the sequence

e t a o n i h s r d l u m w c g f y b p v k x j q z

(1 mark).

Sorting the letters according to their frequency in the complete ciphertext yields instead

l u o g q p d j x m i s h c r k y a n f w t b z e v

(1 mark).

Assuming the distributions match precisely, an ‘l’ in the ciphertext decrypts to an ‘e’ in plaintext, a ‘u’ to a ‘t’, and so on:

l u o g q p d j x m i s h c r k y a n f w t b z e v

e t a o n i h s r d l u m w c g f y b p v k x j q z

This gives the provisional plaintext

breakinf codeh ih gun

(1 mark).

Obviously this is not quite right. It is reasonable to assume that the first word ends in ‘ing’, so the decryption of a ‘y’ to an ‘f’ was wrong. Notice that ‘g’ is adjacent to ‘f’ in frequency of ordinary English, so let’s suppose that those two letters should be transposed. This yields the substitution

l u o g q p d j x m i s h c r k y a n f w t b z e v

e t a o n i h s r d l u m w c f g y b p v k x j q z

and the plaintext

breaking codeh ih fun

It is also reasonable to assume that the ‘h’ in the plaintext should be an ‘s’ (again, these two letters are adjacent in frequency), yielding the final plaintext

breaking codes is fun

(1 mark for the correct plaintext). (Award some marks if they manage to crack the code by any other means; for example, by guessing the plaintext somehow!)