| 1. |
(a) |
(i) What is the contrapositive of
the following statement? |
[2] |
|
|
|
" If n is divisible by 6, then n
is divisible by 2 and n is divisible by 3." |
|
|
|
The
contrapositive is |
|
|
|
|
" If n is
not divisible by 2 or n is not divisible by 3. then n is not divisible
by 6." |
|
|
|
Award one mark
for reversing the antecedent and consequent, with the consequent correctly negated, and
one mark for applying De Morgan correctly; that is, award one mark for |
|
|
|
|
" If ..., then n
is not divisible by 6." |
|
|
|
and one mark
for |
|
|
|
|
" ... n is
not divisible by 2 or n is not divisible by 3..." |
|
|
[2
marks] |
|
|
|
(ii) What is the negation of the
following statement? |
[3] |
|
|
|
" A is a subset of B
and B is a subset of C." |
|
|
|
The
negation is |
|
|
|
|
" A is
not a subset of B or B is not a subset of C." |
|
|
|
Candidates
should also be allowed marks if they make explicit the inclusive nature of the 'or' in the
above statement by writing "or both" at the end. Deduct one mark for any
mistakes. |
|
|
|
[3
marks] |
|
|
|
|
|
|
(b) |
(i) Define the relation that holds
between two integers a and b if and only if a divides b with
no remainder. |
[1] |
|
|
The
relation is |
|
|
|
|
a divides b « b = k * a where k Î Z |
|
|
|
Any
mathematically correct variation should be rewarded with one mark. For example |
|
|
|
|
a divides b « $ k Î Z · b = k * a |
|
|
|
[1
mark] |
|
|
|
|
|
|
|
(ii) Define what it means for this
relation to be transitive. |
[1] |
|
|
Transitivity
is defined as |
|
|
|
|
" a, b, c Î Z · a
divides b Ù b divides c Þ a divides c |
|
|
|
Allow one mark
for appropriate variations. For example, do not penalise the omission of the universal of
the universal quantifier, or the use of English key words instead of the conjunction and
implication: |
|
|
|
|
a divides b and b
divides c implies a divides c |
|
|
[1
mark] |
|
|
|
(iii) Prove that this relation is
transitive. |
[4] |
|
|
Proof of
transitivity: |
|
|
|
|
| a divides b |
|
| « b = k * a where k Î Z |
[by
definition] |
| b divides c |
|
| « c = l * b where l Î Z |
[by
definition] |
| ® c = l * k * a |
[by
substitution] |
| « c = m * a where m Î Z |
|
| « a divides c |
[by
definition] |
|
|
|
|
The
structure of the argument is this: unfold the definition twice, substitute one into the
other, fold up the definition again. Award one mark for each step |
|
|
[4
marks] |
|
|
|
|
|
(c) Suppose that a graph has five
vertices whose degrees are 0, 2, 2, 3 and 9. How many edges does the graph have? |
[2] |
|
The number
of edges may be calculated as |
|
|
|
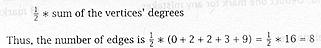 |
|
|
Award one mark
for getting the right formula, and one mark for doing the trivial arithmetic. |
|
|
[2
marks] |
|
|
|
|
|
(d) Use Venn diagrams to show the
following relationships. |
|
|
|
Use Venn
diagrams to show the following relationships. |
|
|
|
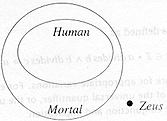
(i) All human beings are mortal.
Zeus is not mortal. |
[2] |
|
|
|
|
|
|
Award one mark
for placing human wholly within Mortal , and one mark for placing Zeus outside Mortal. |
|
|
[2
marks] |
|
|
|
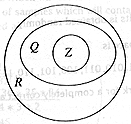
(ii) The set of real number Â, the
set of rational numbers Q, and the set of integers Z. |
[2] |
|
|
|
|
|
|
Award one mark
for placing Q wholly within Â, and one mark for
placing Z wholly within Q. |
|
|
[2
marks] |
|
|
|
|
|
(e) A batch of 100 students' test
papers were each marked by two markers, A and B. Marker A
obtained the statistics: mean = 65, interquartile range = 30, and standard deviation = 5.
If marker B is stricter, such that each student obtains three marks fewer than
those awarded by A, what will B's statistics be? |
|
|
|
(i) mean |
[1] |
|
|
mean = 65
- 3 = 62 |
|
|
[1
mark] |
|
|
|
(ii) interquartile range |
[1] |
|
|
interquartile
range = 30 (same) |
|
|
[1
mark] |
|
|
|
(iii) standard deviation |
[1] |
|
|
standard
deviation = 5 (same) |
|
|
[1
mark] |
|
|
If the
student writes "same" for interquartile range or standard deviation, then accept
it. |
|

