| 2. | (a) A string of three bits is obtained randomly. | |||
| A string of three bits is obtained randomly. | ||||
| (i) List all the elements of the sample space. | [1] | |||
| The sample space is | ||||
| {000, 001, 010, 011, 100, 101, 110, 111} | ||||
| Award one mark for a completely correct answer, none otherwise. | ||||
| [1 mark] | ||||
| (ii) Let A be
the event that the string contains an odd number of 1s, and let B be the event
that the string starts with a 1. Are a and B independent? Explain your answer using probability calculations. |
[4] | |||
| They are independent, as is shown by the fact that | ||||
| Pr(A Ç B) = Pr (A) * Pr (B) | ||||
| By inspection of the sample space, we can see that | ||||
 |
||||
| Award one mark for knowing how to show that the two events are independent (irrespective of whether they claim that they are or not). Award one mark for getting both Pr(A) and Pr(B), one mark for Pr(A Ç B), and one mark for the utterly trivial arithmetic. | ||||
| [4 marks] | ||||
| (b) Suppose that three computer boards in a production run of 40 are defective. A sample of four is to be selected to be checked for defects. | ||||
| There are several different ways of approaching these problems, and any correct method must be rewarded. | ||||
| (i) How many different samples can be chosen? | [2] | |||
| The number of different samples that can be chosen is | ||||
 |
||||
| Award one mark for getting 40C4 and one mark for the arithmetic simplification. | ||||
| [2 marks] | ||||
| (ii) How many samples will contain at least one defective board? | [2] | |||
| The number of samples which will contain no defective boards is 37C4. Therefore, the number of samples which will contain at least one defective board may be calculated as | ||||
 |
||||
| Award one mark for getting a correct method, and a further mark for the arithmetic. | ||||
| [2 marks] | ||||
| (iii) What is the probability that a randomly chosen sample of four contains at least one defective board? | [1] | |||
| The probability that a randomly chosen sample of four contains at least one defective board is simply the ratio of the two precious results | ||||
| Award one mark for getting the correct answer, to two decimal places; no marks otherwise. | ||||
| [1 mark] | ||||
| (c) A coin is tossed 10 times. In each case, the outcome H (for hear), or T (for tail) is recorded. | ||||
| (i) What is the total number of possible outcomes of the coin-tossing experiment? | [2] | |||
| The total number of possible outcomes of the coin-tossing experiment is | ||||
| 210 = 1,024 | ||||
| Award one mark for the correct expression, one mark for the arithmetic. | ||||
| [2 marks] | ||||
| (ii) In how many of the possible outcomes are exactly five heads obtained? | [2] | |||
| The number of outcomes with exactly five five heads obtained is | ||||
 |
||||
| Award one mark for the correct expression, one mark for the arithmetic. | ||||
| [2 marks] | ||||
| (iii) In how many of the possible outcomes are at least nine heads obtained? | [2] | |||
| The number of outcomes with at least nine heads obtained is | ||||
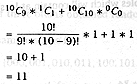 |
||||
| Award one mark for the correct expression, one mark for the arithmetic. | ||||
| [2 marks] | ||||
| (iv) In how many of the possible outcomes are at most one head obtained? | [2] | |||
| The number of outcomes with at most one head obtained is | ||||
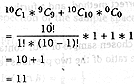 |
||||
| Award one mark for the correct expression, one mark for the arithmetic. | ||||
| [2 marks] | ||||
| (v) In how many of the possible outcomes are at least one tail obtained? | [2] | |||
| The number of outcomes with at least one tail obtained is | ||||
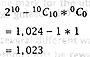 |
||||
| Awarded one mark for the correct expression, one mark for the arithmetic. | ||||
| [2 marks] | ||||