| 3. |
(a) |
(i) Consider the circle relation C
defined for all (x, y) Î Â x Â, such that -1< x, y < 1, |
[3] |
|
|
|
(x, y) Î C « x2 + y2 = 1 |
|
|
|
Is C a function? Why? |
|
|
|
No, it is
not a function. |
|
|
[1
mark] |
|
|
|
Because,
apart from the zeroes, every x is mapped onto two y images. |
|
|
|
Award two
marks for any convincing explanation; for example, |
|
|
|
|
Because C
maps x = 0 onto both y = +1 and y = -1 |
|
|
[2
marks] |
|
|
|
(ii) Consider the relation L
defined for all (x, y) Î Â x Â, |
[3] |
|
|
|
(x, y) Î L « y = x - 1 |
|
|
|
Is C a function? Why? |
|
|
|
Yes, L
is a function. |
|
|
[1 mark] |
|
|
|
Because
every x is mapped onto a unique y image. |
|
|
|
Note: a
universal argument is required; an answer which consists of an example is not good enough. |
|
|
[2
marks] |
|
|
|
|
|
(b) Consider the relation |
|
|
|
B = { (x, y) Î N x N : | x - y | < 2 } |
|
|
Is the relation |
|
|
|
(i) reflexive? |
[2] |
|
|
The
relation is reflexive, |
|
|
[1 mark] |
|
|
|
For every
a Î N, |
|
|
|
|
|a - a| = 0 |
|
|
|
|
« |a - a| < 2 |
|
|
|
|
« (a, a) Î B |
|
|
|
The
essence of the argument is that |a - a| < 2; award
one mark if the candidate gets this right. |
|
|
[1 mark] |
|
|
|
(ii) symmetric? |
[2] |
|
|
The
relation is symmetric. |
|
|
[1 mark] |
|
|
|
For every
a, b Î N, we have |a - b| = |b
- a|; therefore, |
|
|
|
|
(a,b) Î B |
|
|
|
|
« |a - b| < 2 |
|
|
|
|
« |b - a| < 2 |
|
|
|
|
« (b,a) Î B |
|
|
|
The
essence of the argument is that |a - b| = |b - a|; award one mark if the candidate gets this right. |
|
|
[1 mark] |
|
|
|
(iii) transitive? |
[2] |
|
|
The
relation is not transitive. |
|
|
[1 mark] |
|
|
|
As a
counterexample, select |
|
|
|
|
(4, 3) Î B Ù (3,1) Î B |
|
|
|
Notice
that (4,1) Ï B, since |
|
|
|
|
Ø(
|4 - 1| < 2) |
|
|
|
Any counterexample
will do. |
|
|
[1 mark] |
|
|
|
(iv) an equivalence? |
[1] |
|
|
The
relation is not an equivalence, because it is not transitive. |
|
|
[1 mark] |
|
|
|
Award one mark
only if the candidate gets both facts right. |
|
|
Explain your answers. |
|
|
|
|
|
(c) Consider the relation R represented
by the following matrix |
|
|
|
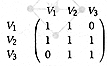 |
|
|
Reward any convincing
arguments in the following. |
|
|
Is the relation |
|
|
|
(i) reflexive? |
[2] |
|
|
R is
reflexive. |
|
|
[1 mark] |
|
|
|
Because
every element is related to itself: the diagonal consists of all 1s. |
|
|
[1 mark] |
|
|
|
(ii) symmetric? |
[2] |
|
|
R is
symmetric. |
|
|
[1 mark] |
|
|
|
Because
the matrix is diagonally symmetric. |
|
|
[1 mark] |
|
|
|
(iii) transitive? |
[2] |
|
|
R is
transitive. |
|
|
[1 mark] |
|
|
|
Because (V1,
V2) = (V2, V3), but (V1, V3) = 0. |
|
|
[1 mark] |
|
|
|
(iv) an equivalence? |
[1] |
|
|
an
equivalence |
|
|
[1
mark] |
|
|
Explain your answers. |
|