| 4. |
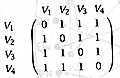
(a) Find the adjacency matrix for |
|
|
|
(i) K4,
the complete graph on four vertices. |
[3] |
|
|
|
 |
|
|
|
Award three
marks for all rows correct: two marks for three rows correct; one mark for two rows
correct; otherwise no marks. |
|
|
[3
marks] |
|
|
|
(ii) K2,3
the complete bipartite graph on (2,3) vertices. |
[3] |
|
|
|
 |
|
|
|
Award three
marks for all rows correct; two marks for four rows correct; one mark for three rows
correct; otherwise no marks. |
|
|
[3
marks] |
|
|
|
|
|
(b) Show that the
following pairs of graphs are not isomorphic by finding an isomorphic invariant that they
do not share. |
|
|
|
(i) |
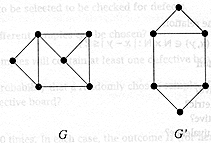
|
[2] |
|
|
G has
nine edges, but G' has only eight edges. |
|
|
|
G has
a vertex of degree four, but G' does not. |
|
|
|
Award two
marks for any correct reason, such as the above two. |
|
|
[2
marks] |
|
|
|
(ii) |
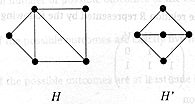
|
[2] |
|
|
H
has a vertex of degree four, but H' does not. |
|
|
|
Award two
marks for any correct reason, such as the above. |
|
|
[2
marks] |
|
|
|
|
|
(c) Show that the two graphs below
are isomorphic by finding the two functions |
|
|
|
g : V( G ) ®
V( G' ) |
|
|
|
h : E( G ) ® E( G' ) |
|
|
by drawing the arrow
diagrams, such that, for all v Î V(G) and e Î E(G)
, v is an endpoint of e iff g(v) is an endpoint of h(e). |
[5] |
|
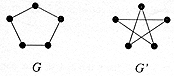
|
|
|
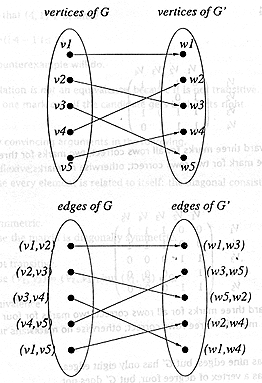
|
|
|
Award one mark
for each pair of correct arrows. |
|
|
[5
marks] |
|
|
|
|
|
(d) Redraw the following bipartite
graphs, so that their bipartite natures are evident. |
[5] |
|
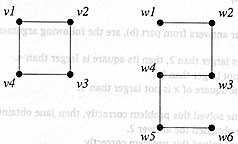
|
|
|
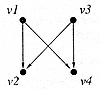
|
|
|
Award one mark
for each correct pair of arrows; maximum two marks. |
|
|
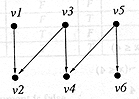
|
|
|
Award three
marks for all arrows correct; two marks for four correct; one mark for two correct; none
otherwise. |
|
|
[5
marks] |
|








