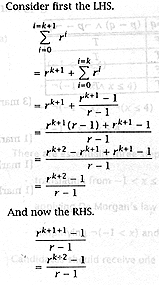| 5. |
(a) Use De Morgan's laws to write
the negation of |
[3] |
|
|
-1 < x < 4 |
|
|
|
Ø (-1 < x < 4) |
|
|
|
« Ø (-1 < x Ù x <
4) |
|
|
|
« Ø (-1 < x) Ú Ø (x
< 4) |
|
|
|
« -1 > x Ú x > 4 |
|
|
There are essentially
three steps in the derivation: |
|
|
|
translating
from -1 < x < 4 to -1 < x Ù x <
4 |
|
|
|
applying
De Morgan's law |
|
|
|
simplifying
Ø (-1 < x) and Ø
(x < 4) |
|
|
Candidates should receive
one mark for each correct step. |
|
|
[3
marks] |
|
|
|
|
|
|
|
(b) Use truth tables to test the
validity of the following arguments. |
|
|
In each of the
following, award three marks for a perfect answer; penalise the candidate by one mark for
each wrong column. |
|
|
|
(i) |
p ® q |
[3] |
|
|
|
q |
|
|
|
|
\ p |
|
|
|
|
| p |
q |
p ® q |
(p ® q) Ù q |
(p ® q) Ù q ® p |
| T |
T |
T |
T |
T |
| T |
F |
F |
F |
T |
| F |
T |
T |
T |
F |
| F |
F |
T |
F |
T |
|
|
|
|
[3
marks] |
|
|
|
(ii) |
p ®
q |
[3] |
|
|
|
ù q |
|
|
|
|
\ ù p |
|
|
|
|
| p |
q |
p ® q |
Øq |
(p ® q) Ù Øq |
Øp |
(p ® q) Ù Øq ® Øp |
| T |
T |
T |
F |
F |
F |
T |
| T |
F |
F |
T |
F |
F |
T |
| F |
T |
T |
F |
F |
T |
T |
| F |
F |
T |
T |
T |
T |
T |
|
|
|
|
[3
marks] |
|
|
|
(iii) |
p ®
q |
[3] |
|
|
|
ù p |
|
|
|
|
\ ù q |
|
|
|
|
| p |
q |
p ® q |
Øp |
(p ® q) Ù Ø p |
Øq |
(p ® q) Ù Øp ® Ø q |
| T |
T |
T |
F |
F |
F |
T |
| T |
F |
F |
F |
F |
T |
T |
| F |
T |
T |
T |
T |
F |
F |
| F |
F |
T |
T |
T |
T |
T |
|
|
|
|
[3
marks] |
|
|
|
|
|
(c) Using your answers from part (b), are the
following arguments valid or not. |
|
|
|
(i) If x is larger than
2, then its square is larger than 4. |
[1] |
|
|
x is not larger than 2 |
|
|
|
\The
square of x is not larger than 4. |
|
|
|
From
b(iii), the argument is false. |
|
|
|
[1
mark] |
|
|
|
(ii) If Jane solved this problem
correctly, then Jane obtained the answer 2. |
[1] |
|
|
Jane obtained the answer 2. |
|
|
|
\Jane
solved this problem correctly. |
|
|
|
From b(i),
the argument is false. |
|
|
|
[1
mark] |
|
|
|
(iii) If this is a dog, then it
has four legs. |
[1] |
|
|
It does not have four legs. |
|
|
|
\It is
not a dog. |
|
|
|
From
b(ii), the argument is true. |
|
|
|
[1
mark] |
|
|
|
|
|
(d) Prove the following using Mathematical
Induction. |
[4] |
|
|
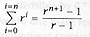 |
|
|
|
What kind of series is this? |
[1] |
|
|
 |
|
|
|
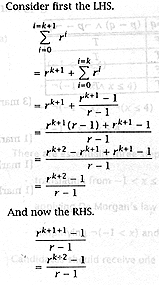 |
|
|
Award one mark
for justifying the basis, and three marks for justifying the inductive step. |
|
|
[4
mark] |
|
|
This is a
geometric series. |
|
|
[1
mark] |
|