December 1998
AP207: ADVANCED PROGRAMMING TECHNIQUES

QUESTION 5

Total Marks: 20 Marks

 Click here to access other questions

Click to access
SUGGESTED SOLUTIONS
for Question 5

 
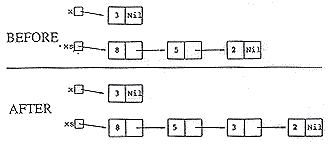
The question is concerned with the implementation of a descending sort procedure that uses the insertion sort algorithm. For example, sorting the sequence [7, 3, 2, 1, 9] produces [9, 7, 3, 2, 1]. The definition of a linked list type, a prototype for the procedure Insert and the procedure InsertSort are given below.

TYPE List = ^Node;
     Node = RECORD
              Item : Integer;
              Next : List
            END;

PROCEDURE Insert(x: List; VAR xs: List);

PROCEDURE InsertionSort(VAR xs: List);
VAR rest, singleton, result: List;
BEGIN
    rest := xs;
    result := Nil;
    WHILE (rest <> Nil) DO
      BEGIN
          singleton := rest;
          rest := rest^.Next;
          singleton^.Next := Nil;
          Insert(singleton, result);
      END
    xs :=  result
END;

The procedure insert (to be defined later) takes a singleton list x and a sorted list xs as its arguments, and inserts the element stored in the singleton list into a sorted list such that the list xs remains in descending sorted order. For example, the figure below shows an example list before and after adding the singleton element 3:

pic4.gif (3117 bytes)
(a) Informally describe the insertion sorting algorithm used in the Pascal procedure InsertionSort above.

 

 [3]
(b) Give the list [2, 5, 1, 4], draw four diagrams that show the states of the lists rest and result immediately after each execution of insert.

 

 [8]
(c) How many list elements would have to be traversed by all the invocations of the insert procedure given:
(i) an already sorted list of size N passed to InsertionSort? i.e., what is the worst case cost, or upper-bound complexiy of insertion sort? [1]
(ii) a list in descending order of values of size N passed to InsertionSort? i.e., what is the best case cost, or lower-bound complexity of insertion sort?

 

 [1]
(d) Define the procedure Insert. [7]