December 1998
AP207: ADVANCED PROGRAMMING TECHNIQUES

QUESTION 4

Total Marks: 20 Marks

 Click here to access other questions

Click to access
SUGGESTED SOLUTIONS
for Question 4

 
(a) Define and explain the properties of a stack abstract data type. In particular, identify any error conditions that may be raised when manipulating a queue.

 

 [3]
The following procedures and functions provide an interface to a stack (of integers) abstract data types:

PROCEDURE CreateStack(VAR stack: StackType);

PROCEDURE Push(VAR stack: StackType; element: Integer);

FUNCTION Pop(VAR stack: StackType):Integer;

FUNCTION IsEmpty(stack: StackType): Boolean;

Given the definition of the procedure anonymous below:

PROCEDURE anonymous(VAR stack: StackType);
VAR temp : StackType;
    element: Integer;
BEGIN
    CreateStack(temp);
    WHILE (not (IsEmpty(stack))) DO
       BEGIN
           element := Pop(stack);
           Push(temp, element);
       END
    stack := temp;
END;

 
(i) What happens if an empty stack is passed to anonymous?

 

 [1]
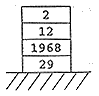
(ii) If the procedure anonymous is passed the stack shown below as an argument, draw the state of the stack on exit from the procedure

pic3.gif (3054 bytes)

 [2]
(iii) Describe the effect of the procedure anonymous when given an arbitrary stack as its argument.

The following questions manipulate a linked-list representation of a stack:

TYPE StackType = ^StackItem;

     StackItem =  RECORD
                      data : Integer;
                      next : StackType;
                   END;

 

 [2]
(c) Using iteration, write a function SizeStack, that has the type shown below, that manipulates the linked-list representation of the StackType, and returns the number of elements in the stack.

FUNCTION SizeStack(stack: StackType):Integer;

 

 [4]
(d) Using recursion, write a function MaxStack, that has the type shown below, that returns the largest integer held in the stack. You can assume that the stack passed as argument to the function contains at least one element.

FUNCTION MaxStack(stack: StackType):Integer;

 

 [4]
(e) Write a function IndexStack, that has the type shown below, that returns the nth element from the top of a non-empty stack (zero is the top of the stack). If n + 1 is greater than the size of the stack, then the function should return the bottom element of the stack.

FUNCTION IndexStack(stack: StackType, n: Integer): Integer;

 [4]