| (a) | The following identities are all laws of Boolean
Algebra:
|
|
(i) Using the identities given below, show that
A +  .B
can be rewritten as A + B, and thus that A + .B = A + B is also a law of
Boolen Algebra. At each stage of your rewriting, you should indicate which identity is
being used.
|
[3] | |
| (ii) By constructing a truth table, show that A
+ A.B = A + B is not a law of Boolean Algebra.
|
[2] | |
| (iii) Complete the following identities to produce the useful laws: | [2] | |
| (1) +
A.B = ... |
||
| (2) A + A. B = ... In each case, the expression on the right should be simpler than that on the left.
|
||
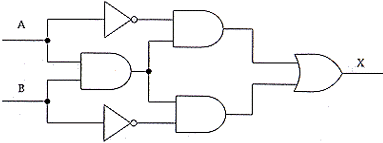
| (iv) Consider the circuit below:
Show how X can be written as a function of inputs A and B, without simplication. Using laws of Boolean algebra, show how this function for X can be simplified as far as possible. Draw a circuit to implement the function with the minimum number of gates.
|
[5] | |
| (b) | The truth table below shows how output Y should
be determined by four inputs A, B, C, and D. An x in the Y column indicates a don't
care condition: the value of Y is not important for the current combination of
inputs.
|
|
| (i) Write out a 4-variable Karnaugh map for this table. | [2] | |
| (ii) By grouping entries in the map, develop a minimal sum-of-products expression for Y in terms of A,B, C and D. | [3] | |
| (iii) Draw a circuit that has Y as an output and A,B,C and D as inputs. | [3] |
