December 1998 LD201: Logic Design (Question 3)

(a)

The following identities are all laws of Boolean Algebra:

pic3a.gif (4545 bytes)

[3]

(i) Using the identities given below, show that A +

.B can be rewritten as A + B, and thus that A +

.B = A + B is also a law of Boolen Algebra. At each stage of your rewriting, you should indicate which identity is being used.

[3]

A + .B
    = (A + ) . (A + B)         [distribution]
    = 1 . (A + B)                    [complementation]
    = A + B                           [dominance]

an equivalent proof using the same set of laws - including De Morgan - should be allowed, as long as every step is properly justified.

if the proof is incorrect, two marks; if it is correct as far as it goes, but is incomplete, one mark for each correctly justified step, to a maximun of two; if it is complete and correct, three marks.

(ii) By constructing a truth table, show that A + A.B = A + B is not a law of Boolean Algebra.

[2]

A	B	A.B	A + A.B	A + B
0	0	0	0	0
0	1	0	0	1
1	0	0	1	1
1	1	1	1	1

one mark for suitable format of table - as long as there are columns for A + A.B and A + B, then that's fine - plus one mark for completely correct set of entries.

(iii) Complete the following identities to produce the useful laws:

[2]

(1) + A.B = + B

(2) A + A. B = A

In each case, the expression on the right should be simpler than that on the left.

one mark each, total two marks; no other answers should be considered.

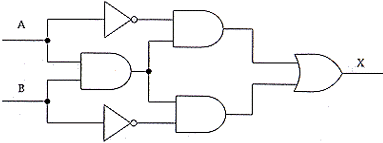
(iv) Consider the circuit below:

pic4.gif (6015 bytes)

Show how X can be written as a function of inputs A and B, without simplication. Using laws of Boolean algebra, show how this function for X can be simplified as far as possible. Draw a cicuit to implement the functino with the minimum number of gates.

X = . (A + B) + . (A + B)

one mark for this answer

. (A + B) + . (A + B)
= . A + . B + . (A + B)                     [distribution]
= 0 + . B + . (A + B)                            [complementation]
= . B + . (A + B)                                  [dominance]
= . B + . A + . B                               [distribution]
= . B + . A + 0                                    [complementation]
= . B + . A                                           [dominance]

if the proof is incorrect, no marks; if it is correct as far as it goes, but is incomplete, one mark for each correctly justified step, to a maximum of two; if it is complete and correct, and every step is justified, three marks.

pic11s.gif (811 bytes)

one mark for drawing an xor gate

[5]

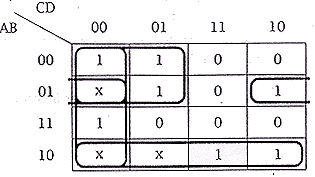
(b)

The truth table below shows how output Y should be determined by four inputs A, B, C, and D. An x in the Y column indicates a don't care condition: the value of Y is not important for the current combination on inputs.

(i) Write out a 4-variable Karnaugh map for this table.

[2]

pic12s.gif (5492 bytes)

one mark for appropriate style of map (AB against CD), one mark for correct entries.

(ii) By grouping entries in the map, develop a minimal sum-of-products expression for Y in terms of A,B, C and D.

[3]

one mark for grouping 1's in the map, one mark for correctly grouping x's as 1's; one mark for the correct sum of products with respect to the map given (note possibility of consequential error - award mark for sum of products if it matches the groups made by the candidate.

Y = . + . + A . + . B .

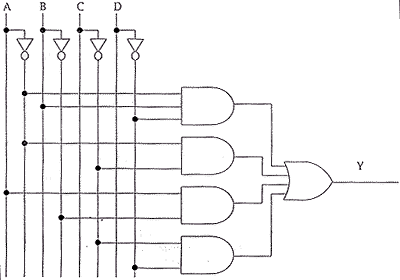
(iii) Draw a circuit that has Y as an output and A,B,C and D as inputs.

[3]

pic14s.gif (7804 bytes)

one mark for appropriate style of circuit, one mark for correct connections, one mark for correct labelling; again, watch for consequential error - circuit should match the sum of products given by the candidate (unless this is completely trivial, in which case it doesn't demonstrate anything)