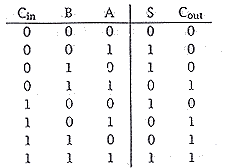
| (a) | (i) A 1-bit full-adder has two binary inputs A and B, a single binary outputs S (for sum) a carry-in, and a carry-out. Copy and complete the following truth table for this component. | [2] |
two marks for a correct table; one mark out of two if the sum and carry columns are reversed.
|
||
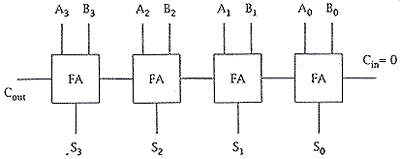
| (ii) Draw and label a diagram to
show how full-adders can be combined to implement a 4-bit parallel adder. A block diagram
for a 4-bit parallel adder is shown below: Your implementation should have the same inputs and outputs as this block diagram.
|
[4] | |
one mark for correct connection of inputs B3B2B1B0 and A3A2A1A0, one mark for carry in set to 1, one mark for correct connection and labelling of output S3S2S1S0, one mark for correct connection of carries, ending with correct carry-out.
|
||
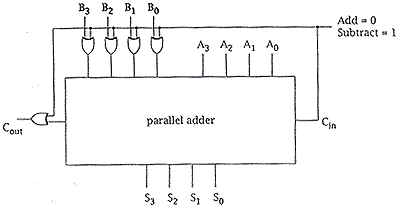
| (iii) Draw and label a diagram to
show how exclusive-or gates can be added to make a 4-bit parallel adder into a 2's
complement parallel adder/substracter. Indicate clearly how the function of the circuit
may be switched between adding and subtracting. When substracting, the carry-out should be treated as a borrow-out: it should be at logic 1 is a borrow condition exists (if the magnitude of B3B2B1B0 is greater than that of A3A2A1A0).
|
[4] | |
one mark for correct connection of xor gates to each of the B inputs, one mark for correct connection of xor gate to carry out, one mark for appropriate labelling of add/substract input to show that add occurs when this input is 0, one mark for correct connection of add/substract input to the carry in.
|
||
| (b) | A binary-coded decimal (BCD) number
is a 4-bit binary number between 0000 and 1001. Two BCD numbers can be added by first
performing binary addition, and then adding 0110 if the result is greater than 1001 or the
binary addition results in a carry-out.
|
|
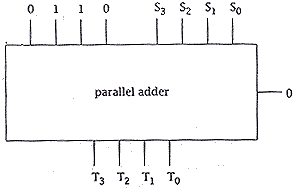
| (i) Draw and label a circuit diagram
to show how a single 4-bit parallel adder can be used to add 0110 to the binary number S3S2S1S0.
Label the BCD result T3T2T1T0, and remember to
set the carry-in to an appropriate value. You may ignore the carry-out. The addition of two BCD numbers results in a carry-out if and only if the correction - the addition of 0110 - is necessary.
|
[2] | |
| one mark for input of 0110
in place of B3B2B1B0,
one mark for setting carry-in to 0.
|
||
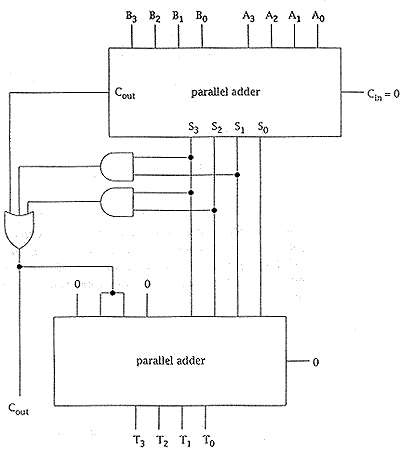
| (ii) Draw and label a circuit diagram to show how two 4-bit parallel adders can be connected to produce a BCD adder. You may use and or or gates if necessary. The BCD adder should have two BCD inputs inputs B3B2B1B0 and A3A2A1A0 and a single BCD output T3T2T1T0. You should also include a carry-in and a carry-out. | [8] | |
this is easier than it looks, and all the information is given in the question one mark for each of the following features:
|