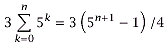December 1999
MA214 : DISCRETE MATHEMATICS

QUESTION 1 (Compulsory)

Total Marks: 30 Marks

• Question 2
• Question 3
• Question 4
• Question 5
• Cover Page

Click to access
SUGGESTED SOLUTIONS
for Question 1

For each of the following sets, determine whether 2 is an element of that set.

(i){x |x is an integer greater than 1 }

(ii){x |x is the square of an integer }

(iii){2, {2} }

(iv){ {2}, { {2} } }

(v){ {2}, {2, {2} } }

(vi){ { {2 } } }

The matrices A and B are given by

(i)Calculate [2 marks ]

(ii)Calculate [2 marks ]

Let p and q be the propositions

p :It is below freezing
q :It is snowing

Write the following propositions using p and q and logical connectives.

(i)It is below freezing and snowing.[1 mark ]

(ii)It is below freezing but not snowing.[1 mark ]

(iii)It is not below freezing and it is not snowing.[1 mark ]

(iv)It is either below freezing or it is snowing, and it is not snowing if it is below freezing.[1 mark ]

(v)It is below freezing precisely when it is snowing.[1 mark ]

A sequence of 10 bits is randomly generated. What is the probability that at least one of these bits is 0?

Use mathematical induction to prove that

whenever n is a nonnegative integer.

Let A be the set {1 ,2 ,3 ,4 }. Which ordered pairs are in the relation

How many ways are there to choose 6 items from 10 distinct items when

(i)the items in the choices are ordered and repetition is not allowed?
[2 marks ]

(ii)the items in the choices are ordered and repetition is allowed?
[2 marks ]

(iii)the items in the choices are unordered and repetition is not allowed?
[2 marks ]