August 1999
LD201 : LOGIC DESIGN

QUESTION 4

Total Marks: 20 Marks

 Click here to access other questions

SUGGESTED SOLUTIONS
Solutions and allocated marks are indicated in green.
Return to Question 4
(a) Give the truth table for a half-adder.|

 [1]
A B C S
0 0 0 0
0 1 0 1
1 0 0 1
1 1 1 0

 
(b) Express the carry and sum terms of a half-adder using NAND and NOT operations only. [2]
For the carry we have
                                    pic14.gif (1315 bytes)
and for the sum we have
                                        pic15.gif (4268 bytes)

 
(c) Hence draw a circuit for a half-adder using only NAND gates. [4]

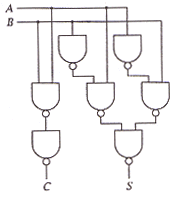
                            pic16.gif (7334 bytes)

 
(d) Show how to construct a full-adder using two half-adders and an OR gate. [3]
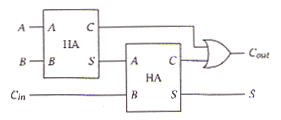
                  pic17.gif (5859 bytes)
(e) Here is the truth table for a 4-to-1 multiplexor.

S1

 S0 B
0 0 A0
0 1 A1
1 0 A2
1 1 A3

(Thus, when S1 = 0 and S0 = 0, the value of B is the same as that of input A0, and so on.) Explain how such a multiplexor can be used to implement an arbitrary 3-input, 1-output circuit.

 [4]

S1 S0 B
0 0 A0
0 1 A1
1 0 A2
1 1 A3

Suppose the three inputs are X, Y, Z. Choose any two of the three inputs (says X, Y) as the selectors. For given values of the selectors(eg X = 0, Y = 0), there are only four possible combinations using Z for the output, namely 0, 1, Z and pic18.gif (60 bytes). It suffices to attach the appropriate combination to each input of the multiplexor.
(f) Hence show how to implement a full-adder using two 4-to-1 multiplexors. [6]

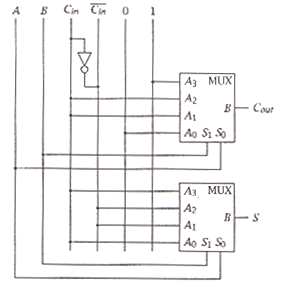                    pic19.gif (16969 bytes)