December 1998
AP207: ADVANCED PROGRAMMING TECHNIQUES

QUESTION 1 (Compulsory)

Total Marks: 20 Marks

 Click here to access other questions

SUGGESTED SOLUTIONS
Solutions and allocated marks are indicated in green.
Return to Question 1

 
(a) Give two distinguishing characteristics (e.g., size, lookup and update policy/efficiency) for each of the following data-structures:
(i) linked-list [2]
  • A dynamically sized data-structure.
  • Indexing is performed from the front of the list.
  • Time for a lookup is proportional to the length of the list.
  • Time for an update is proportional to the length of the list.

1 mark for each of the points above, to a maximum of 2 marks.

 
(ii) array [2]
  • A fixed size data-structure.
  • Any element can be accessed during indexing.
  • Time for a lookup is constant with respect to the size of the array.
  • Time for a update is constant with respect to the size of the array.

1 mark for each of the points above, to a maximum of 2 marks

 
(iii) FIFO queue [2]
  • A dynamically sized data-structure (also award the mark if they say it can be either static or dynamic in size, depending upon the implementation).
  • Access to the elements is in FIFO ordering.
  • Cost of accessing/removing front element is constant.
  • Cost of adding element to the back of the queue is constant.
  • Cost of accessing/removing deeper elements is proportional to the position of the element being removed.

1 mark for each of the points above, to a maximum of 2 marks

 
(iv) LIFO queue [2]
  • A dynamically sized data-structure (also award the mark if they say it can be either static or dynamic in size, depending upon the implementation).
  • Access to the elements is in LIFO ordering.
  • Cost of accessing/removing top element is constant.
  • Cost of accessing/removing deeper elements is proportional to the depth of the element being removed.

1 mark for each of the points above, to a maximum of 2 marks

 
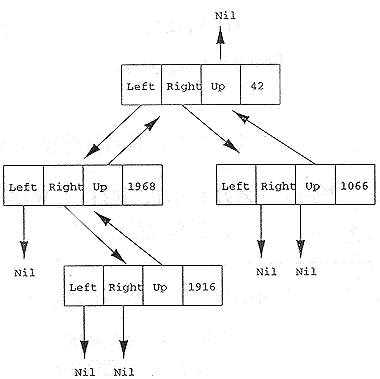
(b) Given the following tree:

pic1.gif (6659 bytes)

 
(i) Write a Pascal type definition, called TreeType that models the tree data-structure shown above.

 

 [3]
Type TreeType = ^NodeType;
     NodeType = Record
                  Left : TreeType;
                  Right : TreeType;
                  Up : TreeType;
                  Data : TreeType;
                End;

One mark should be awarded for having the correct structure to the record; one mark should be awarded for incorporating Data as an integer; one mark should be awarded for having Left, Right, and Up as correct pointers to tree types. The students should not be penalised for using different names for Data, Left, Right, Up, Down or NodeType. If the students obtain half marks for this part of the question, please round their mark up.

 
(ii) What will be printed when the tree shown above is passed to the procedure anonymous below? [2]
PROCEDURE anonymous(VAR root:TreeType);
VAR ptr,copy : TreeTypes;
    BEGIN
    ptr := root;
    WHILE (ptr <> Nil) DO
       BEGIN
       copy := ptr;
       IF (ptr^.Left <> Nil) THEN
           BEGIN
           ptr := ptr^.Left;
           copy^.Left := Nil;
           END
       ELSE
           BEGIN
           IF (ptrv.Right <> Nil) THEN
              BEGIN
              ptr := ptr^.Right;
              copy^.Right := Nil;
              END
           ELSE
              BEGIN
              WRITELN(ptr^.Data);
              ptr := ptr^.Up;
              END
           END
      END
END;
One mark for two lines of numbers. Please award no half marks:

1916
1968
1066
42

 
(iii) Does the procedure anonymous print out the integers held in the tree in a prefix, infix, or postfix style? [1]
Postfix style

 
(iv) What effect does the procedure have on the tree root? [1]
The procedure destroys the tree by overwriting the left and right fields of each node.

 
(v) Write a reursive procedure that performs a preorder traversal of the tree, printing out the integers held within the tree during the traversal. [5]
A sample definition of the pre-order recursive printing procedure is shown below:

Procedure preOrder(root: Tree);
Begin
   If (root <> NIL) Then
   Begin
      WriteLn(root^.Data);
      preOrder(root^.Left);
      preOrder(root^.Right);
   End;
End;

and the following marking scheme should be used:

  • one mark for the procedure declaration
  • one mark for identifying the base case of the recursive as a Nil tree;
  • one mark if the first statement executed when passed a non-empty tree is a recursive call that passes the left sub-tree as its argument.
  • one mark if the second statement executed when passes a non-empty tree is a recursive call that passes the right subtree as its argument.
  • one mark if the third statement executed when passed a non-empty tree is some kind of output statement that prints the data stored in a branch.

do not deduct marks for trivial syntactic errors when marking the above points.