December 1998
AP207: ADVANCED PROGRAMMING TECHNIQUES

QUESTION 4

Total Marks: 20 Marks

 Click here to access other questions

SUGGESTED SOLUTIONS
Solutions and allocated marks are indicated in green.
Return to Question 4

 
(a) Define and explain the properties of a queue abstract data type. In particular, identify any error conditions that may be raised when manipulating a queue. [3]
Properties of a stack.
  • A stack is a last-in first-out data structure
  • Data is only accessible at the top of the stack
  • The items that have been in the stack the longest will be at the bottom (from study guide)
  • it is an error to "pop" an entry from an empty stack
  • it is an error to enquire what the top entry of  an empty stack is

one mark for each point, up to a maximum of three marks.

 
(b) The following procedures and functions provide an interface to a stack (of integers) abstract data types:

PROCEDURE CreateStack(VAR stack: StackType);

PROCEDURE Push(VAR stack: StackType; element: Integer);

FUNCTION Pop(VAR stack: StackType):Integer;

FUNCTION IsEmpty(stack: StackType): Boolean;

Given the definition of the procedure anonymous below:

PROCEDURE anonymous(VAR stack: StackType);
VAR temp : StackType;
    element: Integer;
BEGIN
    CreateStack(temp);
    WHILE (not (IsEmpty(stack))) DO
       BEGIN
           element := Pop(stack);
           Push(temp, element);
       END
    stack := temp;
END;

 
(i) What happens if an empty stack is passed to anonymous? [1]
if an empty stack is passed to anonymous, then an empty stack will be returned.

 
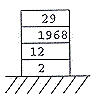
(ii) If the procedure anonymous is passed the stack shown below as an argument draw the state of the stack on exit from the procedure [2]
Two marks for the following picture of the reversed stack:

pic4s.gif (937 bytes)
(iii) Describe the effect of the procedure anonymous when given an arbitrary stack as its argument.

The following questions manipulate a linked-list representation of a stack:

TYPE StackType = StackItem;

StackItem =  RECORD
                data : Integer;
                next : StackType;
             END:

 

 [2]
The procedure anonymous reverses the elements on the stack.

 
(c) Using iteration, write a function SizeStack, that has the type shown below, that manipulates the linked-list representation of the StackType, and returns the number of elements in the stack.

FUNCTION SizeStack(stack: StackType):Integer;

 

 [4]
A definition of SizeStack is shown below:

FUNCTION SizeStack(stack: StackType):Integer;
VAR ptr: StackType;
BEGIN
   SizeStack := 0;
   ptr := stack;
   WHILE (ptr <> Nil) DO
      BEGIN
      ptr : = ptr^.next;
      SizeStack := SizeStack + 1;
   END
END;

  • one mark for returning 0 for an empty stack.
  • one mark for the correct termination condition when iterating down the stack.
  • one mark for iterating down the stack.
  • one mark for keeping count of how many items are on the stack.

 
(d) Using recursion, write a function MaxStack, that has the type shown below, that returns the largest integer held in the stack. You can assume that the stack passed as argument to the function contains at least one element.

FUNCTION MaxStack(stack: StackType):Integer;

 

 [4]
FUNCTION MaxStack(stack: StackType):Integer;
VAR rest:Integer;
BEGIN
   IF (stack^.next=Nil) THEN
      MaxStack := stack^.data;
   ELSE
      BEGIN
      rest := MaxStack(stack^.next);
      IF (rest>stack^.data)
         MaxStack := rest;
      ELSE
         MaxStack := stack^.data;
      END
END;
  • one mark for returning the data element for a singleton stack.
  • one mark for the recursive call down the rest of the stack
  • one mark for checking the result of the recursive call with the current data item
  • one mark for returning the larger of the result from the recursive call, or the current data item

 
(e) Write a function IndexStack, that has the type shown below, that returns the nth element from the top of a non-empty stack (zero is the top of the stack). If n + 1 is greater than the size of the stack, then the function should return the bottom element of the stack.

FUNCTION IndexStack(stack: StackType, n: Integer): Integer;

 

 [4]
A definition of IndexStack is shown below:

FUNCTION IndexStack(stack: StackType, n: Integer): Integer;
Var ptr: StackType;
   i: Integer;
Begin
   i := 0;
   ptr := stack;
   WHILE (i<=n AND ptr^.next<>Nil) DO
      BEGIN
      i := i + 1;
      ptr := ptr^.next;
      END
   IndexStack := ptr^.data;
END;

and the following marking scheme should be used:

  • two marks for a correct conditional within the while loop.
  • one mark for a correct body of the loop
  • one mark for returning the correct data element.